题目内容
10.在函数$y=\frac{{\sqrt{x}}}{x-2}+{(x+1)^0}$中,自变量x的取值范围是x≥0且x≠2.分析 根据被开方数大于等于0,分母不等于0,零指数幂的底数不等于0列式计算即可得解.
解答 解:由题意得,x≥0且x-2≠0,x+1≠0,
解得x≥0且x≠2,x≠-1,
所以,x≥0且x≠2.
故答案为:x≥0且x≠2.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )| A. | BC=FD,AC=ED | B. | ∠A=∠DEF,AC=ED | C. | AC=ED,AB=EF | D. | ∠ABC=∠EFD,BC=FD |
18.已知反比例函数y=$\frac{1}{x}$,下列结论中不正确的是( )
| A. | 图象经过点(-$\frac{1}{2}$,-2) | B. | 图象位于第一、三象限 | ||
| C. | y随x的增大而减小 | D. | 当1<x<3时,y的取值范围是$\frac{1}{3}$<y<1 |
5.一组数据3、4、x、1、4、3有唯一的众数3,则这组数据的中位数是( )
| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( )
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( ) 如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方形的个数最少有( )个.
如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方形的个数最少有( )个.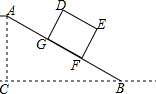 如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号)
如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号) 如图,直线l1∥l2,∠2=40°,则∠1+∠3+∠4=220°.
如图,直线l1∥l2,∠2=40°,则∠1+∠3+∠4=220°.