题目内容
15.化简求值:$\frac{a-3}{a-2}÷(\frac{5}{2-a}+a+2)$,其中a满足:|a+1|是4的算术平方根.分析 先根据分式混合运算的法则把原式进行化简,再根据|a+1|是4的算术平方根求出a的值,把合适的a的值代入原式进行计算即可.
解答 解:原式=$\frac{a-3}{a-2}$÷$\frac{5+(2+a)(2-a)}{2-a}$
=$\frac{a-3}{a-2}$÷$\frac{5+4-{a}^{2}}{2-a}$
=$\frac{a-3}{a-2}$•$\frac{a-2}{(a+3)(a-3)}$
=$\frac{1}{{a{+}3}}$.
∵|a+1|是4的算术平方根,
∴|a+1|=2,解得a1=-3,a2=1.
∵a=-3时,原式结果无意义,
∴当a=1时,原式=$\frac{1}{4}$.
点评 本题考查的是分式的化简求值,在解答此类题目时要注意未知数的取值要保证分式有意义.

练习册系列答案
相关题目
6. 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )
 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
3.$-\frac{3}{4}$的倒数是( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
7.下列各数中,是无理数的( )
| A. | 0 | B. | 2π | C. | $\sqrt{4}$ | D. | $\frac{7}{3}$ |
4.在某次体育测试中,九(一)班五位同学的立定跳远成绩(单位:m)分别为:1.71,1.85,1.85,1.95,2.10,则这组数据的中位数是( )
| A. | 1.71 | B. | 1.85 | C. | 1.90 | D. | 2.10 |
5.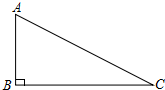 如图,△ABC中,∠B=90°,AB=1,BC=2,则cosA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则cosA=( )
 如图,△ABC中,∠B=90°,AB=1,BC=2,则cosA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则cosA=( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{1}{2}$ |