题目内容
18.已知反比例函数y=$\frac{1}{x}$,下列结论中不正确的是( )| A. | 图象经过点(-$\frac{1}{2}$,-2) | B. | 图象位于第一、三象限 | ||
| C. | y随x的增大而减小 | D. | 当1<x<3时,y的取值范围是$\frac{1}{3}$<y<1 |
分析 根据反比例函数的性质:反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.凡是反比例函数图象上的点,横纵坐标之积=k进行分析即可.
解答 解:A、-$\frac{1}{2}$×(-2)=1,因此反比例函数y=$\frac{1}{x}$经过点(-$\frac{1}{2}$,-2),说法正确,故此选项不合题意;
B、反比例函数y=$\frac{1}{x}$,图象位于第一、三象限,说法正确,故此选项不合题意;
C、反比例函数y=$\frac{1}{x}$,在每一个象限内,y随x的增大而减小,原题说法错误,故此选项符合题意;
D、当1<x<3时,y的取值范围是$\frac{1}{3}$<y<1,说法正确,故此选项不合题意;
故选:C.
点评 此题主要考查了反比例函数的性质,关键是掌握反比例函数y=$\frac{k}{x}$(k≠0),当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小,注意“在每一个象限”这几个字.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )
 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过点D的切线PD与直线AB交于点P,则sin∠ADP的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
3.$-\frac{3}{4}$的倒数是( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
7.下列各数中,是无理数的( )
| A. | 0 | B. | 2π | C. | $\sqrt{4}$ | D. | $\frac{7}{3}$ |
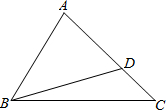 如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线. 如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.
如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.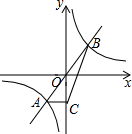 如图,正比例函数y=kx(k>0)和反比例函数y=$\frac{6}{x}$的图象交于A、B两点,过点A作AC⊥y轴于点C,则△ABC的面积为6.
如图,正比例函数y=kx(k>0)和反比例函数y=$\frac{6}{x}$的图象交于A、B两点,过点A作AC⊥y轴于点C,则△ABC的面积为6.