题目内容
19.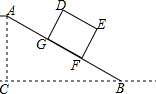 如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号)
如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号)
分析 作DH⊥BC,垂足为H,且与AB相交于S.证出∠GDS=∠SBH,根据$\frac{GS}{GD}$=$\frac{1}{2}$,得到GD=1m,利用勾股定理求出DS的长,然后求出BS=5m,进而求出HS,然后得到DH.
解答  解:作DH⊥BC,垂足为H,且与AB相交于S.
解:作DH⊥BC,垂足为H,且与AB相交于S.
∵∠DGS=∠BHS,∠DSG=∠BSH,
∴∠GDS=∠SBH,
∴$\frac{GS}{GD}$=$\frac{1}{2}$,
∵DG=EF=2m,
∴GS=1m,
∴DS=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$m,BS=BF+FS=3.5+(2.5-1)=5m,
设HS=xm,则BH=2xm,
∴x2+(2x)2=52,
∴x=$\sqrt{5}$m,
∴DH=$\sqrt{5}$+$\sqrt{5}$=2$\sqrt{5}$m.
故答案是:2$\sqrt{5}$.
点评 本题考查了解直角三角形的应用--坡度坡角问题,熟悉坡度坡角的定义和勾股定理是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
7.下列各数中,是无理数的( )
| A. | 0 | B. | 2π | C. | $\sqrt{4}$ | D. | $\frac{7}{3}$ |
14.若实数m=$\sqrt{18}-\sqrt{8}$,则估计m的值所在范围正确的是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
4.在某次体育测试中,九(一)班五位同学的立定跳远成绩(单位:m)分别为:1.71,1.85,1.85,1.95,2.10,则这组数据的中位数是( )
| A. | 1.71 | B. | 1.85 | C. | 1.90 | D. | 2.10 |
 如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.
如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.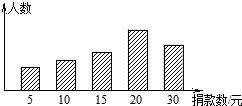 孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.
孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.