题目内容
20. 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( )
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据等腰三角形的性质求出∠B=∠C,即可判断①;根据等腰直角三角形求出AP⊥BC,AP=$\frac{1}{2}$BC=PC,∠BAP=∠CAP=45°=∠C,求出∠FPC=∠EPA,根据ASA推出△APE≌△CPF,推出AE=CF,PE=PF,S△APE=S△CPF,再逐个判断即可.
解答 解:∵△ABC中,AB=AC,∠BAC=90°,
∴∠B=∠C=$\frac{1}{2}×$(180°-90°)=45°,∴①正确;
:∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴AP⊥BC,AP=$\frac{1}{2}$BC=PC,∠BAP=∠CAP=45°=∠C.
∵∠APF+∠FPC=90°,∠APF+∠APE=90°,
∴∠FPC=∠EPA,
在△APE和△CPF中,
$\left\{\begin{array}{l}{∠EAP=∠C}\\{AP=PC}\\{∠EPA=∠FPC}\end{array}\right.$,
∴△APE≌△CPF(ASA),
∴AE=CF,∴②正确;
PE=PF,
∵∠EPF=90°,
∴△EPF是等腰直角三角形,∴③正确;
∵△APE≌△CPF,
∴S△APE=S△CPF,
∵BP=CP,
∴S△APC=$\frac{1}{2}$S△ABC,
∴四边形AEPF的面积是
S=S△APE+S△APF
=S△CPF+S△APF
=S△APC
=$\frac{1}{2}$S△ABC,∴④正确;
即正确的有4个.
故选D.
点评 本题考查了全等三角形的性质和判定,直角三角形的性质,等腰三角形的性质的应用,能求出△APE≌△CPF是解此题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
11.方程组$\left\{\begin{array}{l}{2x+y=4}\\{x+3z=1}\\{x+y+z=7}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=2}\\{z=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=8}\\{z=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=2}\\{z=2}\end{array}\right.$ |
12.下列根式中属最简二次根式的是( )
| A. | $\sqrt{13}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\frac{1}{{\sqrt{2}}}$ |
 如图,已知直线y=kx+b与双曲线y=$\frac{m}{x}$(x<0)交于A(x1,y1),B(x2,y2),且x1≠x2,直线AB交x轴于点C(x0,0).
如图,已知直线y=kx+b与双曲线y=$\frac{m}{x}$(x<0)交于A(x1,y1),B(x2,y2),且x1≠x2,直线AB交x轴于点C(x0,0).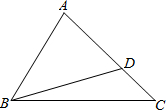 如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线. 如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.
如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.