题目内容
4.观察:①$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}=1+\frac{1}{1}-\frac{1}{1+1}=1\frac{1}{2}$:
②$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}=1+\frac{1}{2}-\frac{1}{2+1}=1\frac{1}{6}$:
③$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}=1+\frac{1}{3}-\frac{1}{3+1}=1\frac{1}{12}$.
按照上面的规律$\sqrt{1+\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}}$=1$\frac{1}{20}$.
当n为正整数时,$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$的值为1$\frac{1}{n(n+1)}$.
分析 根据题中给出的列子找出规律即可得出结论.
解答 解:观察:
①$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}=1+\frac{1}{1}-\frac{1}{1+1}=1\frac{1}{2}$:
②$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}=1+\frac{1}{2}-\frac{1}{2+1}=1\frac{1}{6}$:
③$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}=1+\frac{1}{3}-\frac{1}{3+1}=1\frac{1}{12}$.
∴$\sqrt{1+\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}}$=1+$\frac{1}{4}$-$\frac{1}{4+1}$=1$\frac{1}{20}$,
当n为正整数时,$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=1$\frac{1}{n(n+1)}$.
故答案为:1$\frac{1}{20}$,1$\frac{1}{n(n+1)}$.
点评 本题考查的是二次根式的性质与化简,根据题意找出规律是解答此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
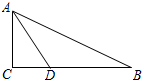 已知在Rt△ABC中,∠C=90°,∠CAB=2∠B,∠A的角平分线AD交BC于D,点D到AB的距离是2cm,求BC的长.
已知在Rt△ABC中,∠C=90°,∠CAB=2∠B,∠A的角平分线AD交BC于D,点D到AB的距离是2cm,求BC的长. 已知:AB=AC,∠BAC=50°,求$\widehat{AB},\widehat{BC},\widehat{CA}$的度数.
已知:AB=AC,∠BAC=50°,求$\widehat{AB},\widehat{BC},\widehat{CA}$的度数.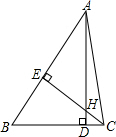 如图所示,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于H,若AE=CE,求证:△AEH≌△CEB.
如图所示,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于H,若AE=CE,求证:△AEH≌△CEB.