题目内容

15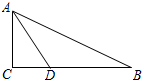．已知在Rt△ABC中，∠C=90°，∠CAB=2∠B，∠A的角平分线AD交BC于D，点D到AB的距离是2cm，求BC的长．

分析 根据角平分线的性质得到CD=DE=2cm，根据直角三角形的性质求出BD的长，计算得到答案．

解答 解：作DE⊥AB于E，
∵∠C=90°，∠CAB=2∠B，
∴∠B=30°，
∵AD是∠A的角平分线，∠C=90°，DE⊥AB，
∴CD=DE=2cm，
∵∠C=90°，∠B=30°，
∴BD=2DE=4cm，
∴BC=CD+BD=6cm．
答：BC的长为6cm．

点评 本题考查的是角平分线的性质和直角三角形的性质，掌握角的平分线上的点到角的两边的距离相等、在直角三角形中，30°所对的直角边是斜边的一半是解题的关键．

练习册系列答案
相关题目
5．等式[（-8.3）-□]÷（-6$\frac{2}{7}$）=0中，□表示的数是-8.3．
6．如图△ABC≌△A′B′C′，AA′∥BC，∠ABC=70°，求∠CBC′的大小．
3．已知实数x满足$\sqrt{4{x}^{2}+18-12\sqrt{2}x}$=2x+3$\sqrt{2}$，那么x的取值范围是x=0．
10．当a＞0，b＞0，则$\frac{|a|}{a}+\frac{|b|}{b}$=2．
20．已知a+$\frac{1}{a}$=6，求$\sqrt{a}$-$\frac{1}{\sqrt{a}}$的值．
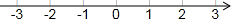7．利用勾股定理在如图所示的数轴上找出数-$\sqrt{5}$，-2$\sqrt{2}$和$\sqrt{2}+1$对应的点．并标在数轴上．
4．观察：
①$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}=1+\frac{1}{1}-\frac{1}{1+1}=1\frac{1}{2}$：
②$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}=1+\frac{1}{2}-\frac{1}{2+1}=1\frac{1}{6}$：
③$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}=1+\frac{1}{3}-\frac{1}{3+1}=1\frac{1}{12}$．
按照上面的规律$\sqrt{1+\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}}$=1$\frac{1}{20}$．
当n为正整数时，$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{（n+1）^{2}}}$的值为1$\frac{1}{n（n+1）}$．
5．若|a|=2，b的相反数是最大的负整数，c是绝对值最小的数，则-a+b-c的值为（　　）
A．0B．3或-1C．2D．-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网