已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=-=$\frac{m}{n}$.且b+d+f+-+n≠0.试说明$\frac{a+c+e+-+m}{b+d+f+-+n}$=$\frac{a}{b}$．题目和参考答案——青夏教育精英家教网—

题目内容

12．已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=…=$\frac{m}{n}$，且b+d+f+…+n≠0，试说明$\frac{a+c+e+…+m}{b+d+f+…+n}$=$\frac{a}{b}$．

分析根据等比性质，可得答案．

解答证明：设$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=…=$\frac{m}{n}$=k，
∴a=bk，c=dk，e=fk…m=nk，
∴$\frac{a+c+e+…+m}{b+d+f+…+n}$=$\frac{bk+dk+fk+…+nk}{b+d+f+…+n}$=k=$\frac{a}{b}$．

点评本题考查了比例的性质，利用等比性质是解题关键．

练习册系列答案

3．已知实数x满足$\sqrt{4{x}^{2}+18-12\sqrt{2}x}$=2x+3$\sqrt{2}$，那么x的取值范围是x=0．

20．已知a+$\frac{1}{a}$=6，求$\sqrt{a}$-$\frac{1}{\sqrt{a}}$的值．

7．

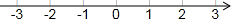利用勾股定理在如图所示的数轴上找出数-$\sqrt{5}$，-2$\sqrt{2}$和$\sqrt{2}+1$对应的点．并标在数轴上．

17．设x₁，x₂是方程ax²+bx+c=0的两根，求证：
（1）x₁²+x₂²=$\frac{{b}^{2}-2ac}{{a}^{2}}$；
（2）$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}+\frac{b}{c}$=0．

4．观察：
①$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}=1+\frac{1}{1}-\frac{1}{1+1}=1\frac{1}{2}$：
②$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}=1+\frac{1}{2}-\frac{1}{2+1}=1\frac{1}{6}$：
③$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}=1+\frac{1}{3}-\frac{1}{3+1}=1\frac{1}{12}$．
按照上面的规律$\sqrt{1+\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}}$=1$\frac{1}{20}$．
当n为正整数时，$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{（n+1）^{2}}}$的值为1$\frac{1}{n（n+1）}$．

1．

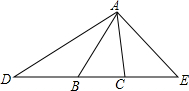如图，△ABC中，∠ACB=80°，延长CB至D，使DB=BA，延长BC至E，使CE=CA．连接AD，AE，若∠DAE=115°，试说明△ABC是等腰三角形．

2．不解方程，判断下列一元二次方程根的情况，
（1）x²-kx+k²+1=0；
（2）x²+kx-k-2=0．

试题分类