Question

14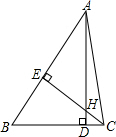．如图所示，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE相交于H，若AE=CE，求证：△AEH≌△CEB．

Answer 1

分析 由同角的余角相等可得∠EAH=∠ECB，而AE=CE，∠AEH=∠CEB=90°，根据ASA即可证明△AEH≌△CEB．

解答 证明：∵AD⊥BC，CE⊥AB，垂足分别为D，E，
∴∠AEH=∠CEB=90°，∠EAH=90°-∠B，∠ECB=90°-∠B，
∴∠EAH=∠ECB．
在△AEH与△CEB中，
$\left\{\begin{array}{l}{∠EAH=∠ECB}\\{AE=CE}\\{∠AEH=∠CEB=90°}\end{array}\right.$，
∴△AEH≌△CEB（ASA）．

点评 此题主要考查了全等三角形的判定，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．