题目内容
16.不改变分式的值,把下列分式的分子、分母中次数最高的项的系数都化为正数.①$\frac{-{x}^{2}}{{x}^{2}-y}$;②$\frac{b}{-{a}^{2}-a}$;③$\frac{1-x-{x}^{2}}{1+x-{x}^{2}}$;④-$\frac{3m-{m}^{2}}{1-{m}^{2}}$.
分析 首先将分子、分母均按同一字母的降幂排列,若第一项的系数为负,则添带负号的括号.本题特别注意分子、分母和分式本身的符号的改变.
解答 解:①$\frac{-{x}^{2}}{{x}^{2}-y}$=-$\frac{{x}^{2}}{{x}^{2}-y}$;
②$\frac{b}{-{a}^{2}-a}$=-$\frac{b}{{a}^{2}+a}$;
③$\frac{1-x-{x}^{2}}{1+x-{x}^{2}}$=$\frac{-{x}^{2}-x+1}{-{x}^{2}+x+1}$=$\frac{{x}^{2}+x-1}{{x}^{2}-x-1}$;
④-$\frac{3m-{m}^{2}}{1-{m}^{2}}$=-$\frac{-{m}^{2}+3m}{-{m}^{2}+1}$=-$\frac{{m}^{2}-3m}{{m}^{2}-1}$.
点评 本题考查了分式的基本性质,同类分式中的操作可总结成口诀:“一排二添三变”,“一排”即按同一个字母的降幂排列;“二添”是把第一项系数为负号的分子或分母添上带负号的括号;“三变”是按分式变号法则把分子与分母的负号提到分式本身的前边.分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变.

练习册系列答案
相关题目
5.若|a|=2,b的相反数是最大的负整数,c是绝对值最小的数,则-a+b-c的值为( )
| A. | 0 | B. | 3或-1 | C. | 2 | D. | -1 |
 如图△ABC≌△A′B′C′,AA′∥BC,∠ABC=70°,求∠CBC′的大小.
如图△ABC≌△A′B′C′,AA′∥BC,∠ABC=70°,求∠CBC′的大小.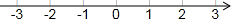 利用勾股定理在如图所示的数轴上找出数-$\sqrt{5}$,-2$\sqrt{2}$和$\sqrt{2}+1$对应的点.并标在数轴上.
利用勾股定理在如图所示的数轴上找出数-$\sqrt{5}$,-2$\sqrt{2}$和$\sqrt{2}+1$对应的点.并标在数轴上.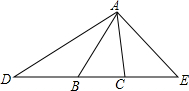 如图,△ABC中,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA.连接AD,AE,若∠DAE=115°,试说明△ABC是等腰三角形.
如图,△ABC中,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA.连接AD,AE,若∠DAE=115°,试说明△ABC是等腰三角形.