题目内容
15．某公司现有组合材料200箱，每箱500元，又以800元每箱的价格购进60箱B材料，准备用这两种材料由甲、乙两车间生产机器人扫地器，并且B材料要求全部用完，甲车间用一箱B材料和组合材料4箱可生产出机器人扫地器12个，乙车间用一箱B材料和组合材料2箱可生产出的机器人扫地器比甲车间少2个．（1）该公司甲车间最多能生产机器人扫地器多少个？
（2）若机器人扫地器售价为2000元/个，那么该公司如何分配两车间的生产任务，才能使这次生产所能获取的利润最大？最大利润是多少？
分析 （1）设甲车间使用了x箱B材料，则乙车间使用了（60-x）箱B材料，根据使用组合材料不超过200箱即可得出关于x的一元一次不等式，解之即可得出x的取值范围，进而即可得出12x的最大值；
（2）设利润为y元，根据利润=销售价格-成本价即可得出y关于x的一次函数关系式，根据一次函数的性质即可解决最值问题．
解答 解：（1）设甲车间使用了x箱B材料，则乙车间使用了（60-x）箱B材料，
∵4x+2（60-x）≤200，
∴x≤40，
∴12x≤480．
答：该公司甲车间最多能生产机器人扫地器480个．
（2）设利润为y元，
结合（1）可得：y=2000×[12x+（12-2）（60-x）]-60×800-500×[4x+2（60-x）]=3000x+1092000，
∵k=3000＞0，
∴当x=40时，y取最大值，最大值为1212000．
答：当甲车间使用40箱B材料、乙车间使用20箱B材料时，才能使这次生产所能获取的利润最大，最大利润为1212000元．
点评 本题考查了一次函数的应用以及一元一次不等式的应用，解题的关键是：（1）根据使用组合材料不超过200箱列出关于x的一元一次不等式；（2）根据利润=销售价格-成本价找出y关于x的一次函数关系式．
练习册系列答案
相关题目
6．嘉淇同学大学毕业后借助低息贷款创业，他向银行贷款30000元，分12个月还清贷款，月利率是0.2%，银行规定的还款方式为“等额本金法”，即每月除归还等额的本金为30000÷12=2500元外，还需要归还本月还款前的本金的利息，下面是还款的部分明细．
第1个月，由于本月还款前的本金是30000元，则本月应归还的利息为30000×0.2%=60元，本月应归还的本息和为2500+60=2560元；
第2个月，由于本月还款前的本金是27500元，则本月应归还的利息为27500×0.2%=55元，本月应归还的本息和为2500+55=2555元．
…
根据上述信息，则
（1）在空格处直接填写结果：
（2）设第x个月应归还的利息是y元，求y关于x的函数关系式，并写出x的取值范围；
（3）嘉淇将创业获利的2515元用于还款，则恰好可以用于还清第几个月的本息和？
第1个月，由于本月还款前的本金是30000元，则本月应归还的利息为30000×0.2%=60元，本月应归还的本息和为2500+60=2560元；
第2个月，由于本月还款前的本金是27500元，则本月应归还的利息为27500×0.2%=55元，本月应归还的本息和为2500+55=2555元．
…
根据上述信息，则
（1）在空格处直接填写结果：
| 月数 | 第1个月 | 第2个月 | … | 第5个月 | … |
| 还款前的本金（单位：元） | 30000 | 27500 | … | 20000 | … |
| 应归还的利息（单位：元） | 60 | 55 | … | 40 | … |
（3）嘉淇将创业获利的2515元用于还款，则恰好可以用于还清第几个月的本息和？
3．2015杭州国际动漫节为期6天，某动漫企业准备了卡通玩偶、cosplay道具、动漫手环三类产品参加市集展卖活动，其中动漫手环备货720件，三类产品备货数量的统计图如图甲所示．销售人员（销售卡通玩偶3人，销售cosplay道具1人，销售动漫手环2人）在展卖期间的前3天每人每天销售数量统计图如图乙所示，三类产品前3天的销售总量见表格．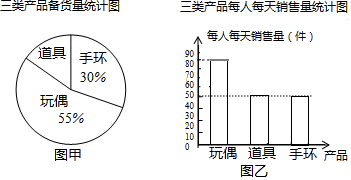
（1）求卡通玩偶、cosplay道具各备货多少件？并直接写出m的值；
（2）若销售人员不变，销售速度相同，请通过计算说明三类产品在展卖期间是否售完？若没有，则求出剩下产品的名称及剩余的数量．
| 产品 | 前三天销售总量（件） |
| 玩偶 | 720 |
| 道具 | m |
| 手环 | 300 |
（2）若销售人员不变，销售速度相同，请通过计算说明三类产品在展卖期间是否售完？若没有，则求出剩下产品的名称及剩余的数量．
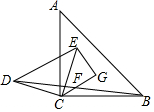如图，△ABC和△DEC都是等腰直角三角形，连接BD，F是BD的中点，连接CF并延长至G，使FG=CF，连接EC，CE=10，CF=4，EG=6，则S△ABC=2$\sqrt{130}$．