题目内容
10．已知x为任意实数，化简：$\sqrt{{x}^{2}-2x+1}$+$\sqrt{{x}^{2}+6x+9}$．分析 利用当x≥1时，当-3＜x＜1时，当-3≥x时，分别化简求出答案．
解答 解：$\sqrt{{x}^{2}-2x+1}$+$\sqrt{{x}^{2}+6x+9}$
=$\sqrt{（x-1）^{2}}$+$\sqrt{（x+3）^{2}}$
当x≥1时，原式=x-1+x+3=2x+2；
当-3＜x＜1时，原式=-（x-1）+（x+3）=4；
当-3≥x时，原式=-（x-1）-（x+3）=-2x-2．
点评 此题主要考查了二次根式的化简，正确分类讨论是解题关键．
练习册系列答案
相关题目
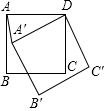如图，边长为4的正方形ABCD绕点D旋转30°后能与四边形A′B′C′D重合．
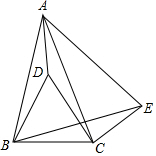如图，在△ABC中，AB=AC，点D在△ABC内，BD=BC，∠DBC=60°，点E在△ABC外，∠BCE=150°，∠ABE=60°．