题目内容
7.某中学为丰富学生的课余生活,准备购买一批每副售价50元的羽毛球拍和每筒售价10元的羽毛球.购买时,发现商场正在进行两种优惠促销活动.甲;买一副羽毛球拍送一筒羽毛球;
乙:按购买金额打9折付款.
学校欲购买这种羽毛球拍10副,羽毛球x(x≥10)筒.
(1)写出每种优优惠办法实际付款金额y甲(元)、y乙(元)与x(筒)之间的函数关系式.
(2)当购买同样多的羽毛球时,按哪种优惠办法购买更省钱?
(3)如果商场允许可以任意选择一种优惠办法购买,也可以同时用两种优惠办法购买,那么购买这种羽毛球拍10副,羽毛球60筒.哪种购买方案最省钱.
分析 (1)根据题意可以分求得y甲(元)、y乙(元)与x(筒)之间的函数关系式;
(2)根据(1)中的函数关系式,利用分类讨论的数学思想可以解答本题;
(3)根据题意可以分别计算出各种方案的花费情况,即可解答本题.
解答 解:(1)由题意可得,
y甲=50×10+(x-10)×10=10x+400,
y乙=(50×10+10x)×0.9=9x+450,
即y甲=10x+400,y乙=9x+450;
(2)当10x+400<9x+450,
解得,x<50,
当10x+400=9x+450,
解得,x=50,
当10x+400>9x+450,
解得,x>50,
由上可得,当购买不足50筒羽毛球时,甲种优惠办法更省钱;当购买50筒羽毛球时,两种优惠办法一样;当购买多于50筒羽毛球时,乙种优惠办法更省钱;
(3)当选择甲种购买方案时,花费为:10x+400=10×60+400=1000,
当选择乙种购买方案时,花费为:9x+450=9×60+450=990,
当选择两种方案时,花费最低为:10×50+(60-10)×10×0.9=950,
由上可得,同时用两种优惠办法购买最省钱.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,利用分类讨论和函数的数学思想解答本题.

练习册系列答案
相关题目
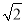 的倒数是( )
的倒数是( )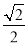 B.
B. 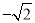 C.
C. 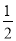 D.
D. 
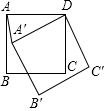 如图,边长为4的正方形ABCD绕点D旋转30°后能与四边形A′B′C′D重合.
如图,边长为4的正方形ABCD绕点D旋转30°后能与四边形A′B′C′D重合.