题目内容
6.已知:x=$\sqrt{2}$-$\sqrt{3}$,y=$\sqrt{2}$+$\sqrt{3}$,求下列各式的值(1)x2-2xy+y2
(2)x2-y2.
分析 (1)直接利用完全平方公式将原式变形进而代入求出答案;
(2)直接利用平方差公式将原式变形进而代入求出答案.
解答 解:(1)x2-2xy+y2
=(x-y)2
把x=$\sqrt{2}$-$\sqrt{3}$,y=$\sqrt{2}$+$\sqrt{3}$代入得:
原式=[($\sqrt{2}$-$\sqrt{3}$)-($\sqrt{2}$+$\sqrt{3}$)]2
=12;
(2)x2-y2=(x+y)(x-y)
=[($\sqrt{2}$-$\sqrt{3}$)-($\sqrt{2}$+$\sqrt{3}$)][($\sqrt{2}$-$\sqrt{3}$)+($\sqrt{2}$+$\sqrt{3}$)]
=-2$\sqrt{3}$×2$\sqrt{2}$
=-4$\sqrt{6}$.
点评 此题主要考查了二次根式的化简求值,正确应用乘法公式是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 如图,线段DE由线段AB平移而得,AB=4,EC=7-CD,则△DCE的周长为11 cm.
如图,线段DE由线段AB平移而得,AB=4,EC=7-CD,则△DCE的周长为11 cm.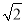 的倒数是( )
的倒数是( )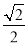 B.
B. 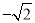 C.
C. 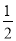 D.
D. 
 已知函数y=mx2+(2m+1)x+2(m为实数).
已知函数y=mx2+(2m+1)x+2(m为实数).