题目内容
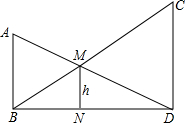如图，已知AB⊥BD，CD⊥BD，MN⊥BD，且AB=10，CD=20，求h的值．考点：平行线分线段成比例
专题：计算题
分析：根据平行线的性质由AB⊥BD，MN⊥BD得到AB∥MN，再根据平行于三角形一边的直线截其他两边（或两边的延线），所得的对应线段成比例得到
=
，同理得到
=
，然后把两式相加可得
+
=1，再解h的一次方程即可．
| MN |
| AB |
| DN |
| BD |
| MN |
| CD |
| BN |
| BD |
| h |
| 10 |
| h |
| 20 |
解答：解：∵AB⊥BD，MN⊥BD，
∴AB∥MN，
∴
=
，
∵CD⊥BD，MN⊥BD，
∴MN∥CD，
∴
=
，
∴
+
=
+
=
=1，
∴
+
=1，
∴h=
．
∴AB∥MN，
∴
| MN |
| AB |
| DN |
| BD |
∵CD⊥BD，MN⊥BD，
∴MN∥CD，
∴
| MN |
| CD |
| BN |
| BD |
∴
| MN |
| AB |
| MN |
| CD |
| BN |
| BD |
| DN |
| BD |
| BN+DN |
| BD |
∴
| h |
| 10 |
| h |
| 20 |
∴h=
| 20 |
| 3 |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例；如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边．
练习册系列答案
名校课堂系列答案
相关题目
已知平行四边形ABCD中，E为AD的中点，AF：BF=2：3，求AG：GC的值．
如图，在△ABC中，AD平分∠BAC，交BC于点D，BE⊥AD，交AD的延长线于点E，BF=EF．求证：EF∥AC．