题目内容
 如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD,交AD的延长线于点E,BF=EF.求证:EF∥AC.
如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD,交AD的延长线于点E,BF=EF.求证:EF∥AC.考点:三角形中位线定理,等腰三角形的判定与性质
专题:证明题
分析:根据等边对等角可得∠BEF=∠EBF,再根据等角的余角相等求出∠EAF=∠AEF,然后根据角平分线的定义可得∠EAF=∠CAD,从而得到∠AEF=∠CAD,再根据内错角相等,两直线平行证明即可.
解答:证明:∵BF=EF,
∴∠BEF=∠EBF,
∵BE⊥AD,
∴∠EAF+∠EBF=∠AEF+∠BEF,
∴∠EAF=∠AEF,
∵AD平分∠BAC,
∴∠EAF=∠CAD,
∴∠AEF=∠CAD,
∴EF∥AC.
∴∠BEF=∠EBF,
∵BE⊥AD,
∴∠EAF+∠EBF=∠AEF+∠BEF,
∴∠EAF=∠AEF,
∵AD平分∠BAC,
∴∠EAF=∠CAD,
∴∠AEF=∠CAD,
∴EF∥AC.
点评:本题考查了等腰三角形的判定与性质,平行线的判定,角平分线的定义,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
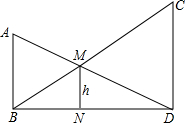 如图,已知AB⊥BD,CD⊥BD,MN⊥BD,且AB=10,CD=20,求h的值.
如图,已知AB⊥BD,CD⊥BD,MN⊥BD,且AB=10,CD=20,求h的值.