题目内容
 已知平行四边形ABCD中,E为AD的中点,AF:BF=2:3,求AG:GC的值.
已知平行四边形ABCD中,E为AD的中点,AF:BF=2:3,求AG:GC的值.考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:首先延长FE交CD于点H,由四边形ABCD是平行四边形,易证得△AEF∽△DEH,△AFG∽△CHG,又由E为AD的中点,AF:BF=2:3,根据相似三角形的对应边成比例,即可求得答案.
解答: 解:延长FE交CD于点H,
解:延长FE交CD于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△AEF∽△DEH,△AFG∽△CHG,
∴AE:DE=DH:AF,
∵E为AD的中点,
∴DH=AF,
∵△AFG∽△CHG,
∴AG:GC=AF:CH,
∵AF:BF=2:3,
∴AF:AB=2:5,
∴AF:CH=2:7,
∴AG:GC=2:7.
 解:延长FE交CD于点H,
解:延长FE交CD于点H,∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△AEF∽△DEH,△AFG∽△CHG,
∴AE:DE=DH:AF,
∵E为AD的中点,
∴DH=AF,
∵△AFG∽△CHG,
∴AG:GC=AF:CH,
∵AF:BF=2:3,
∴AF:AB=2:5,
∴AF:CH=2:7,
∴AG:GC=2:7.
点评:此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
不改变原式的值,将6-(+3)-(-7)+(-2)中的减法改成加法并写成省略加号和括号的形式是( )
| A、-6-3+7-2 |
| B、6-3-7-2 |
| C、6-3+7-2 |
| D、6-3-7-2 |
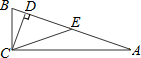 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,点E是AB中点,AB=10,则线段DE的长度为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,点E是AB中点,AB=10,则线段DE的长度为( )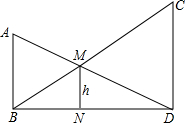 如图,已知AB⊥BD,CD⊥BD,MN⊥BD,且AB=10,CD=20,求h的值.
如图,已知AB⊥BD,CD⊥BD,MN⊥BD,且AB=10,CD=20,求h的值.