题目内容
19.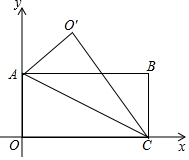 如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
分析 解法一:如图作O′M⊥OC于M,交AB于N,想办法求出OM,O′M即可;
解法二:求出直线OO′与直线AC的交点G的坐标,利用中点坐标公式即可解决问题;
解答 解法一:如图作O′M⊥OC于M,交AB于N,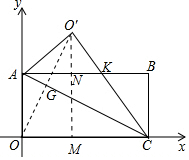
易知AK=CK,设AK=CK=x,
在Rt△BCK中,x2=(6-x)2+32,
解得x=$\frac{15}{4}$,
∴AK=$\frac{15}{4}$,
在Rt△AO′K中,O′K=$\sqrt{A{K}^{2}-AO{′}^{2}}$=$\frac{9}{4}$,
∵$\frac{1}{2}$•AO′×O′K=$\frac{1}{2}$•AK•O′N,
∴O′N=$\frac{9}{5}$,
在Rt△ANO′中,AN=$\sqrt{AO{′}^{2}-O′{N}^{2}}$=$\frac{12}{5}$,
∴OM=AN=$\frac{12}{5}$,O′M=$\frac{24}{5}$,
∴O′($\frac{12}{5}$,$\frac{24}{5}$).
解法二:易知直线AC的解析式为y=-$\frac{1}{2}$x+3,
∴直线OO′的解析式为y=2x,
由$\left\{\begin{array}{l}{y=2x}\\{y=-\frac{1}{2}x+3}\end{array}\right.$解得G($\frac{6}{5}$,$\frac{12}{5}$),
∵OG=O′G,
∴O′($\frac{12}{5}$,$\frac{24}{5}$).
点评 主要考查翻折变换、坐标与图形的性质、一次函数的应用、矩形的性质、勾股定理.相似三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
10.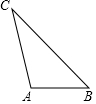 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三个内角角平分线的交点 |
14.关于x的一元二次方程(a+1)x2-x+a2-2a-2=0,有一个根是1,则a=( )
| A. | -1 | B. | 2 | C. | 2或-1 | D. | -2或1 |
4.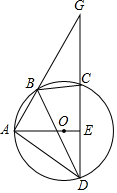 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )| A. | 50° | B. | 60° | C. | 80° | D. | 90° |
11.下列各式化简后的结果为3$\sqrt{2}$的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{36}$ |
8.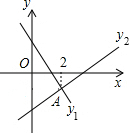 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )| A. | k>0 | B. | m>n | C. | 当x<2时,y2>y1 | D. | 2k+n=m-2 |
9.三角形的两边a、b的夹角为60°且满足方程x2-3$\sqrt{2}$x+4=0,则第三边的长是( )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |