题目内容
9.三角形的两边a、b的夹角为60°且满足方程x2-3$\sqrt{2}$x+4=0,则第三边的长是( )| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 先利用因式分解法解方程x2-3$\sqrt{2}$x+4=0得到a=2$\sqrt{2}$,b=$\sqrt{2}$,如图,△ABC中,a=2$\sqrt{2}$,b=$\sqrt{2}$,∠C=60°,作AH⊥BC于H,再在Rt△ACH中,利用含30度的直角三角形三边的关系得到CH=$\frac{\sqrt{2}}{2}$,AH=$\frac{\sqrt{6}}{2}$,则BH=$\frac{3\sqrt{2}}{2}$,然后在Rt△ABH中利用勾股定理计算AB的长即可.
解答 解:x2-3$\sqrt{2}$x+4=0,
(x-2$\sqrt{2}$)(x-$\sqrt{2}$)=0,
所以x1=2$\sqrt{2}$,x2=$\sqrt{2}$,
即a=2$\sqrt{2}$,b=$\sqrt{2}$,
如图,△ABC中,a=2$\sqrt{2}$,b=$\sqrt{2}$,∠C=60°,
作AH⊥BC于H,
在Rt△ACH中,∵∠C=60°,
∴CH=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,AH=$\sqrt{3}$CH=$\frac{\sqrt{6}}{2}$,
∴BH=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$,
在Rt△ABH中,AB=$\sqrt{(\frac{\sqrt{6}}{2})^{2}+(\frac{3\sqrt{2}}{2})^{2}}$=$\sqrt{6}$,
即三角形的第三边的长是$\sqrt{6}$.
故选A.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了解直角三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 25元 | B. | 28.5元 | C. | 29元 | D. | 34.5元 |
| 手工制品 | 手串 | 中国结 | 手提包 | 木雕笔筒 |
| 总数量(个) | 200 | 100 | 80 | 70 |
| 销售数量(个) | 190 | 100 | 76 | 68 |
| A. | 手串 | B. | 中国结 | C. | 手提包 | D. | 木雕笔筒 |
 如图,AM为∠BAC的平分线,下列等式错误的是( )
如图,AM为∠BAC的平分线,下列等式错误的是( )| A. | $\frac{1}{2}$∠BAC=∠BAM | B. | ∠BAM=∠CAM | C. | ∠BAM=2∠CAM | D. | 2∠CAM=∠BAC |
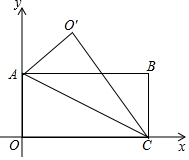 如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.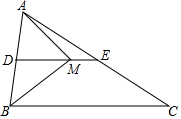 在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8.
在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8.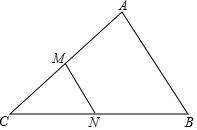 如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3.
如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3. 如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=3.
如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=3.