题目内容
8.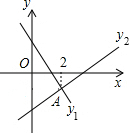 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )| A. | k>0 | B. | m>n | C. | 当x<2时,y2>y1 | D. | 2k+n=m-2 |
分析 直接利用一次函数经过的象限以及图象与坐标轴交点和利用函数图象比较两函数大小方法分别分析得出答案.
解答 解:A、∵直线l2:y=kx+n,图象经过一、三象限,
∴k>0,故选项A正确,不合题意;
B、∵直线l1:y=-x+m图象与y轴交于正半轴为(0,m),直线l2:y=kx+n,图象与y轴交于负半轴(0,n),
∴m>n,故选项B正确,不合题意;
C、∵直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,
∴当x<2时,y2<y1,故此选项错误,符合题意;
D、∵直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,
∴当x=2时,2k+n=m-2,正确,不合题意.
故选:C.
点评 此题主要考查了一次函数的性质以及一次函数图象,正确利用数形结合分析是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
18.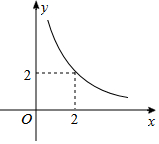 设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
 设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )| A. | 4 | B. | 5 | C. | 5或3$\sqrt{2}$ | D. | 4或3$\sqrt{2}$ |
3. 阅读下列材料:
阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
下面是小明的探究过程,请补充完整:
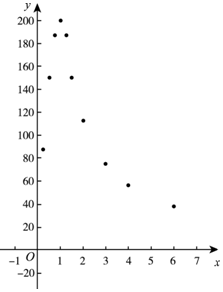
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
 阅读下列材料:
阅读下列材料:实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
| 饮酒后的时间x (小时) | … | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ | 1 | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | 6 | … |
| 血液中酒精含量y (毫克/百毫升) | … | $\frac{175}{2}$ | 150 | $\frac{375}{2}$ | 200 | $\frac{375}{2}$ | 150 | $\frac{225}{2}$ | $\frac{225}{3}$ | $\frac{225}{4}$ | 45 | $\frac{225}{6}$ | … |
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
20.为了满足顾客的需求,某商场将5kg奶糖,3kg酥心糖和2kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后什锦糖的售价应为每千克( )
| A. | 25元 | B. | 28.5元 | C. | 29元 | D. | 34.5元 |
17.今年5月21日是全国第27个助残日,某地开展“心手相连,共浴阳光”为主题的手工制品义卖销售活动.长江特殊教育学校将同学们手工制作的手串、中国结、手提包、木雕笔筒的相关销售信息汇总如下表,其中销售率最高的是( )
| 手工制品 | 手串 | 中国结 | 手提包 | 木雕笔筒 |
| 总数量(个) | 200 | 100 | 80 | 70 |
| 销售数量(个) | 190 | 100 | 76 | 68 |
| A. | 手串 | B. | 中国结 | C. | 手提包 | D. | 木雕笔筒 |
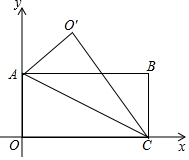 如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.