题目内容
4.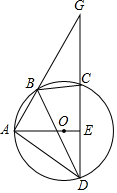 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )| A. | 50° | B. | 60° | C. | 80° | D. | 90° |
分析 根据四点共圆的性质得:∠GBC=∠ADC=50°,由垂径定理得:$\widehat{CM}=\widehat{DM}$,则∠DBC=2∠EAD=80°.
解答  解:如图,∵A、B、D、C四点共圆,
解:如图,∵A、B、D、C四点共圆,
∴∠GBC=∠ADC=50°,
∵AE⊥CD,
∴∠AED=90°,
∴∠EAD=90°-50°=40°,
延长AE交⊙O于点M,
∵AO⊥CD,
∴$\widehat{CM}=\widehat{DM}$,
∴∠DBC=2∠EAD=80°.
故选C.
点评 本题考查了四点共圆的性质:圆内接四边形的任意一个外角等于它的内对角,还考查了垂径定理的应用,属于基础题.

练习册系列答案
相关题目
15.下列运算或变形正确的是( )
| A. | -2a+2b=-2(a+b) | B. | a2-2a+4=(a-2)2 | C. | (2a2)3=6a6 | D. | 3a2•2a3=6a5 |
12.化化工产品C是由A,B两种原料加工而成的,每个C产品的质量为50kg,经测定加工费与A的质量的平方成正比例;A原料的成本10元/kg,B原料的成本:40元/kg;这种C产品中A的含量不能低于10%,又不能高于60%;C产品的出厂价经核算是含B的质量的一次函数.经市场调查,当含A的质量不高于8kg时:利润=出厂价-成本;当含A的质量不低于8kg时,每个C产品的利润将与含A的质量成反比例.
下表是每个C产品的成本及出厂价一览表的一部分.
(1)求出每个C产品的成本y(元)与含A的质量x(kg)之间的函数关系式,并写出x的范围;(每个C成本=A的成本+B的成本+加工费用);
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
下表是每个C产品的成本及出厂价一览表的一部分.
| 含A:10% | 含A(30%) | |
| 成本(元/个) | 1875 | 1775 |
| 出厂价 | 2450 | 2350 |
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
9.下列运算正确的是( )
| A. | $\frac{3a+b}{6}$=$\frac{a+b}{2}$ | B. | 2×$\frac{a+b}{3}$=$\frac{2a+b}{3}$ | C. | $\sqrt{{a}^{2}}$=a | D. | |a|=a(a≥0) |




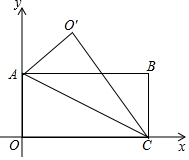 如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.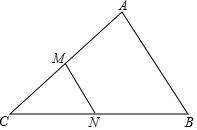 如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3.
如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3.