题目内容
14.关于x的一元二次方程(a+1)x2-x+a2-2a-2=0,有一个根是1,则a=( )| A. | -1 | B. | 2 | C. | 2或-1 | D. | -2或1 |
分析 根据一元二次方程的解的定义,把x=1代入(a+1)x2-x+a2-2a-2=0得关于a的方程,然后解关于a的方程后利用一元二次方程的定义确定满足条件的a的值.
解答 解:把x=1代入(a+1)x2-x+a2-2a-2=0得a+1-1+a2-2a-2=0,
整理得a2-a-2=0,解得a=2或a=-1,
而a+1≠0,
所以a的值为2.
故选B.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
相关题目
9.用计算器计算时,下列说法错误的是( )
| A. | 计算“$\frac{1}{2}$-1$\frac{3}{4}$”的按键顺序是 | |
| B. | 计算“3×105-28”的按键顺序是 | |
| C. | “已知SinA=0.3,求锐角A”的按键顺序是 | |
| D. | 计算“($\frac{1}{2}$)5”的按键顺序是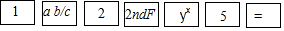 |
3. 阅读下列材料:
阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
下面是小明的探究过程,请补充完整:
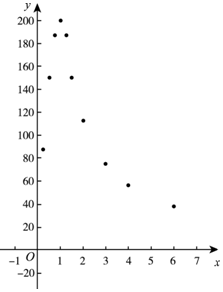
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
 阅读下列材料:
阅读下列材料:实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
| 饮酒后的时间x (小时) | … | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ | 1 | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | 6 | … |
| 血液中酒精含量y (毫克/百毫升) | … | $\frac{175}{2}$ | 150 | $\frac{375}{2}$ | 200 | $\frac{375}{2}$ | 150 | $\frac{225}{2}$ | $\frac{225}{3}$ | $\frac{225}{4}$ | 45 | $\frac{225}{6}$ | … |
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
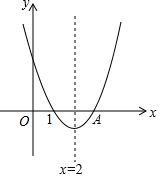 二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),根据图象解答下列问题:
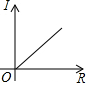
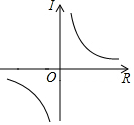
二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),根据图象解答下列问题: 一次函数y=ax+b和反比例函数y=$\frac{b}{x}$在同一坐标系内的大致图象如图所示,则a<0,b>0.
一次函数y=ax+b和反比例函数y=$\frac{b}{x}$在同一坐标系内的大致图象如图所示,则a<0,b>0. 如图,Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是6.
如图,Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是6.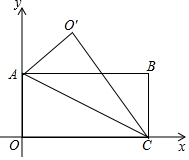 如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
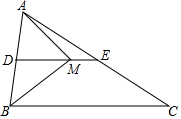 在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8.
在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8.