题目内容
7.某机床加工一批机器零件,如果每小时加工30个,那么12小时可以完成.(1)设每小时加工x个零件,所需时间为y小时,写出y与x之间的函数关系式,画出图象;
(2)若要在一个工作日(8小时)内完成,每小时要比原来多加工几个?
分析 (1)根据题意可以得到y与x的函数解析式,并画出函数的图象;
(2)根据(1)中的函数解析式可以求得当y=8时的x的值,然后与30作差即可解答本题.
解答  解:(1)由题意可得,
解:(1)由题意可得,
y=$\frac{30×12}{x}=\frac{360}{x}$,
即y与x的函数关系式是y=$\frac{360}{x}$,函数图象如右图所示;
(2)由题意可得,
$\frac{360}{8}-30=45-30$=15,
答:每小时要比原来多加工15个.
点评 本题考查反比例函数的应用,解答本题的关键是明确题意,写出相应的函数解析式,利用反比例函数的性质解答.

练习册系列答案
相关题目
18.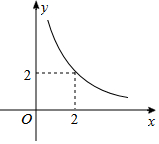 设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
 设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )| A. | 4 | B. | 5 | C. | 5或3$\sqrt{2}$ | D. | 4或3$\sqrt{2}$ |
15.下列运算或变形正确的是( )
| A. | -2a+2b=-2(a+b) | B. | a2-2a+4=(a-2)2 | C. | (2a2)3=6a6 | D. | 3a2•2a3=6a5 |
12.化化工产品C是由A,B两种原料加工而成的,每个C产品的质量为50kg,经测定加工费与A的质量的平方成正比例;A原料的成本10元/kg,B原料的成本:40元/kg;这种C产品中A的含量不能低于10%,又不能高于60%;C产品的出厂价经核算是含B的质量的一次函数.经市场调查,当含A的质量不高于8kg时:利润=出厂价-成本;当含A的质量不低于8kg时,每个C产品的利润将与含A的质量成反比例.
下表是每个C产品的成本及出厂价一览表的一部分.
(1)求出每个C产品的成本y(元)与含A的质量x(kg)之间的函数关系式,并写出x的范围;(每个C成本=A的成本+B的成本+加工费用);
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
下表是每个C产品的成本及出厂价一览表的一部分.
| 含A:10% | 含A(30%) | |
| 成本(元/个) | 1875 | 1775 |
| 出厂价 | 2450 | 2350 |
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
17.今年5月21日是全国第27个助残日,某地开展“心手相连,共浴阳光”为主题的手工制品义卖销售活动.长江特殊教育学校将同学们手工制作的手串、中国结、手提包、木雕笔筒的相关销售信息汇总如下表,其中销售率最高的是( )
| 手工制品 | 手串 | 中国结 | 手提包 | 木雕笔筒 |
| 总数量(个) | 200 | 100 | 80 | 70 |
| 销售数量(个) | 190 | 100 | 76 | 68 |
| A. | 手串 | B. | 中国结 | C. | 手提包 | D. | 木雕笔筒 |
 如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1.
如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1. 如图,Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是6.
如图,Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是6.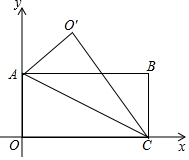 如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.
如图,四边形OABC是矩形,点A(0,3),点C(6,0),以AC为折痕折叠,点O落在点O′的位置,用两种方法求O′坐标.