题目内容
14. 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.(1)若∠1:∠3=3:4,求∠3的度数.
(2)若AB=4.8,AD=6.4,动点P从B点出发以每秒1个单位的速度沿B→E→F的路线运动至F结束,当时间t等于多少时,点P到△BEF的两边的距离相等?
分析 (1)可以假设∠1=3x,∠3=4x,由∠3+∠FEB+∠2=180°,∠2=∠FEB=3x,列出方程即可解决问题.
(2)设AE=a,则EB=ED=6.4-x,在Rt△AEB中,由AB2+AE2=EO2,可得4.82+x2=(6.4-x)2,解方程即可得点E的坐标,作EH⊥OC于H,则四边形AOHE是矩形,EH=OA=4.8,先求出EO、OF,分两种情形①当点P在OE上时,作P1M⊥EF于M,P1N⊥OF于N,根据$\frac{{S}_{△EF{P}_{1}}}{{S}_{△OF{P}_{1}}}$=$\frac{\frac{1}{2}EF•{P}_{1}M}{\frac{1}{2}OF•{P}_{1}N}$=$\frac{{P}_{1}E}{{P}_{1}O}$=$\frac{6}{5}$,由此即可求出OP.②当点P在EF上时,由OE=OF,可知EP2=FP2时,点P到OE,OF两边距离相等,由此即可解决问题.
解答 解:(1)∵∠1:∠3=3:4,
∴可以假设∠1=3x,∠3=4x,
∵四边形ABCD是矩形,
∴AD∥BC,∠DAB=90°,
∴∠2=∠1=3x,
∵∠3+∠FEB+∠2=180°,∠2=∠FEB=3x,
∴4x+3x+3x=180°,
∴x=18°,
∴∠3=4x=72°.
(2)设AE=a,则EB=ED=6.4-x,
在Rt△AEB中,∵AB2+AE2=EO2,
∴4.82+x2=(6.4-x)2,
∴x=1.4,
∴点E坐标(1.4,4.8).
作EH⊥OC于H,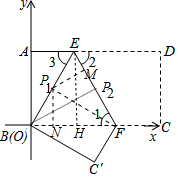
则四边形AOHE是矩形,EH=OA=4.8,
由(2)可知,EO=$\sqrt{A{E}^{2}+O{A}^{2}}$=$\sqrt{4.{8}^{2}+1.{4}^{2}}$=5,
∵∠OEF=∠1,
∴OE=OF=5,
∴EF=$\sqrt{E{H}^{2}+H{F}^{2}}$=$\sqrt{4.{8}^{2}+3.{6}^{2}}$=6.
①当点P在OE上时,作P1M⊥EF于M,P1N⊥OF于N,
如果P1M=P1N,
则有$\frac{{S}_{△EF{P}_{1}}}{{S}_{△OF{P}_{1}}}$=$\frac{\frac{1}{2}EF•{P}_{1}M}{\frac{1}{2}OF•{P}_{1}N}$=$\frac{{P}_{1}E}{{P}_{1}O}$=$\frac{6}{5}$,
∴OP1=$\frac{5}{11}$×5=$\frac{25}{11}$,
∴t=$\frac{25}{11}$s时.
②当点P在EF上时,∵OE=OF,
∴EP2=FP2时,点P到OE,OF两边距离相等,
此时t=5+3=8s.
综上所述,t=$\frac{25}{11}$s或8s时,点P到△BEF的两边的距离相等.
点评 本题考查矩形的性质、坐标与图形的性质、勾股定理、角平分线的性质定理等知识,解题的关键是熟练应用所学知识,学会利用面积法求有关线段.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | 11011001(二进制数) | B. | 75(十进制数) | ||
| C. | 72(八进制数) | D. | 57(十六制数) |
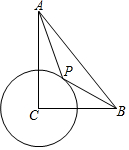 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2 $\sqrt{17}$ | D. | 4 |
 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )| A. | 4 | B. | 5 | C. | 10 | D. | 12 |
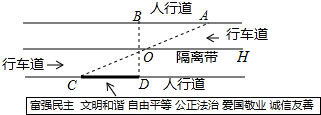 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m.
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m.
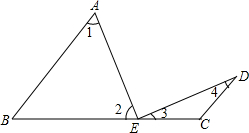 已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.
已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.