题目内容
9.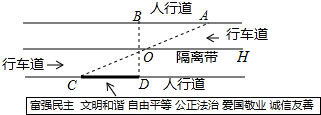 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m.
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m.
分析 根据两平行线间的距离相等得到OB=OD,再由一对直角相等,一对内错角相等,利用ASA得到三角形AOB与三角形COD全等,利用全等三角形对应边相等即可求出CD的长.
解答 解:∵AB∥OH∥CD,相邻两平行线间的距离相等,
∴OB=OD,
∵OB⊥AB,OD⊥DC,
∴∠ABO=∠CDO=90°,
在△ABO和△CDO中,
$\left\{\begin{array}{l}{∠ABO=∠CDO}\\{OB=OD}\\{∠AOB=∠COD}\end{array}\right.$,
∴△ABO≌△CDO(ASA),
∴CD=AB=20m,
故答案为:20
点评 此题考查了全等三角形的应用,垂直定义,以及平行线间的距离,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
4.若函数y=$\left\{\begin{array}{l}{{x}^{2}-2(x≤2)}\\{2x(x>2)}\end{array}\right.$,则当函数值y=8时,自变量x的值是( )
| A. | ±$\sqrt{6}$ | B. | 4 | C. | ±$\sqrt{6}$或4 | D. | 4或-$\sqrt{6}$ |
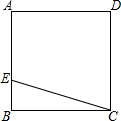 如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?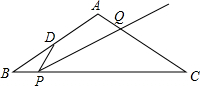 如图,等腰△ABC中,AB=AC=4,BC=m,点D是边AB的中点,点P是边BC上的动点,且不与B、C重合,∠DPQ=∠B,射线PQ交AC于点Q.当点Q总在边AC上时,m的最大值是4$\sqrt{2}$.
如图,等腰△ABC中,AB=AC=4,BC=m,点D是边AB的中点,点P是边BC上的动点,且不与B、C重合,∠DPQ=∠B,射线PQ交AC于点Q.当点Q总在边AC上时,m的最大值是4$\sqrt{2}$. 已知,如图,⊙O的半径为6,弧$\widehat{AC}$的度数为120°,点B为弧$\widehat{AC}$的中点,点D为⊙O上异于A、B、C的三点,OE⊥AD于E,OF⊥CD于F,连接EF.
已知,如图,⊙O的半径为6,弧$\widehat{AC}$的度数为120°,点B为弧$\widehat{AC}$的中点,点D为⊙O上异于A、B、C的三点,OE⊥AD于E,OF⊥CD于F,连接EF. 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置. 如图,正方形ABCD的边长为2,点A与O重合,点C在y轴上,求正方形ABCD各顶点的坐标.
如图,正方形ABCD的边长为2,点A与O重合,点C在y轴上,求正方形ABCD各顶点的坐标.