题目内容
19.阅读材料:如图1,四边形ABCD的对角线AC,BD交于点O,点M是AB边上的一点,过点M分别作ME∥BD,MF∥AC交直线AC,BD于点E,F,显然四边形OEMF是平行四边形.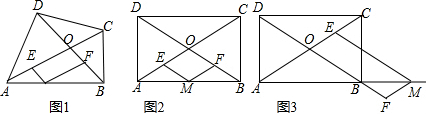
探究发现:
(1)当对角线AC,BD满足AC⊥BD时,四边形OEMF是矩形.
(2)如图2,若四边形ABCD是矩形,且M是AB的中点,判断四边形OEMF是什么特殊的平行四边形,并写出证明过程.
拓展延伸:
(3)如图3,在四边形ABCD为矩形的条件下,若点M是边AB延长线上的一点,此时OA,ME,MF三条线段之间存在怎样的数量关系?并说明理由.
分析 (1)由矩形的判断方法即可,
(2)由三角形的中位线判断出ME=MF,得到邻边相等平行四边形是菱形;
(3)先判断出四边形OEMF是平行四边形,再由平行四边形的性质得到EA=EM,即可.
解答 (1)解:要使平行四边形OEMF是矩形,
∴∠AOB=90°,
∴AC⊥BD,
故答案为AC⊥BD.
(2)四边形OEMF是菱形.
证明:
在矩形ABCD中,OA=OB,
∵点M是AB的中点,ME∥BD,MF∥AC,
∴ME=$\frac{1}{2}$OB,MF=$\frac{1}{2}$OA,
∴ME=MF,
∵四边形OEMF是平行四边形,
∴四边形OEMF是菱形.
(3)解:MF+OA=ME,
理由:在矩形ABCD中,OA=OB,
∵ME∥BD,MF∥AC,
∴四边形OEMF是平行四边形,
∴MF=EO,
∴∠OAB=∠OBA=∠EMA,
∴EA=EM,
∵MF=OE,
∴MF+OA=ME
点评 本题是四边形的比较简单的综合题,主要考查了特殊的四边形的性质和判定,解本题的关键是熟练特殊四边形的性质和判定,本题的疑点是特殊四边形的性质和判定的区别.

练习册系列答案
相关题目
9.(-a)n+a(-a)n-1的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | (-1)n-1 |
7. 如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
 如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )| A. | 40° | B. | 70° | C. | 80° | D. | 140° |
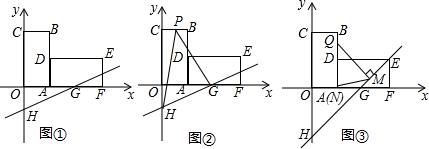
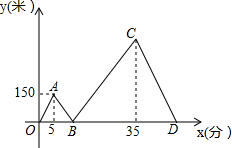 甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.
甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示. 如图,抛物线y=-x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).
如图,抛物线y=-x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6). 我们可以计算出
我们可以计算出