题目内容
14.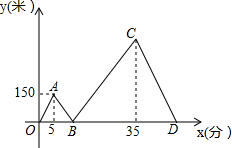 甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.
甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.(1)求甲、乙两人行走的速度;
(2)当乙到达图书馆时,求甲、乙两人间的距离;
(3)求线段BC所在直线对应的函数表达式.
分析 (1)根据速度=$\frac{路程}{时间}$,即可解决问题.
(2)用总路程减去甲走的路程即可.
(3)设解析式为y=kx+b,把C、B两点代入即可.
解答 解:(1)V甲=$\frac{150}{5}$=30(米/分),V乙=$\frac{1500}{35-5}$=50米/分.
(2)1500-30×35=450米.
则当乙到达图书馆时,甲、乙两人间的距离为350米.
(3)设线段BC所在直线对应的函数表达式为y=kx+b.
由题意点B坐标(12.5,0),
将(12.5,0),(35,450)代入y=kx+b
得$\left\{\begin{array}{l}{12.5k+b=0}\\{35k+b=450}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=20}\\{b=-250}\end{array}\right.$,
故线段BC所在直线对应的函数表达式为y=20x-250.
点评 本题考查一次函数的应用,解题的关键是熟练掌握路程、速度、时间的关系,学会用待定系数法确定函数解析式,属于中考常考题型.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
| A. | 当a<1时,点B在⊙A外 | B. | 当1<a<5时,点B在⊙A内 | ||
| C. | 当a<5时,点B在⊙A内 | D. | 当a>5时,点B在⊙A外 |
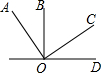 如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.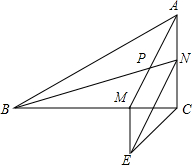 如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,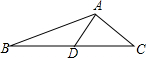 如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.
如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$. 如图,一束平行太阳光照射到正方形上,若∠α=28°,则∠β=62°.
如图,一束平行太阳光照射到正方形上,若∠α=28°,则∠β=62°.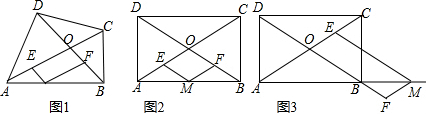
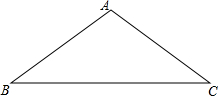 如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.
如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.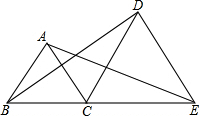 点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.
点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.