题目内容
19.若关于x、y的二元一次方程组$\left\{\begin{array}{l}3x+y=1+a\\ x+3y=3\end{array}\right.$的解满足x+y<2,求a的取值范围.分析 把a看做已知数表示出方程组的解,代入已知不等式求出a的范围即可.
解答 解:方程组$\left\{\begin{array}{l}3x+y=1+a\\ x+3y=3\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=\frac{3}{8}a\\ y=1-\frac{1}{8}a\end{array}\right.$,
∴x+y=1+$\frac{1}{4}$a,
∵x+y<2,
∴1+$\frac{1}{4}$a<2,
解得:a<4.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
14.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
| A. | 当a<1时,点B在⊙A外 | B. | 当1<a<5时,点B在⊙A内 | ||
| C. | 当a<5时,点B在⊙A内 | D. | 当a>5时,点B在⊙A外 |
4.平方根与立方根相等的数是( )
| A. | 1 | B. | 0 | C. | 1和0 | D. | 0,1 |
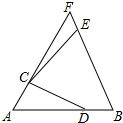 如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.
如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.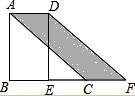 如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.
如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.
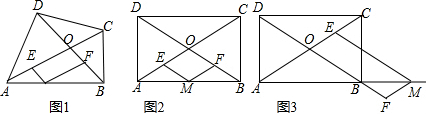
 如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).
如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).