题目内容
20.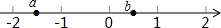 我们可以计算出
我们可以计算出①$\sqrt{{2}^{2}}$=2 $\sqrt{(\frac{2}{3})^{2}}$=$\frac{2}{3}$;$\sqrt{{3}^{2}}$=3
而且还可以计算$\sqrt{(-2)^{2}}$=2$\sqrt{(-{\frac{2}{3})}^{2}}$=$\frac{2}{3}$$\sqrt{(-3)^{2}}$=3
(1)根据计算的结果,可以得到:①当a>0时$\sqrt{{a}^{2}}$=a;②当a<0时$\sqrt{{a}^{2}}$=-a.
(2)应用所得的结论解决:如图,已知a,b在数轴上的位置,化简$\sqrt{a^2}$-$\sqrt{b^2}$-$\sqrt{{{(a+b)}^2}}$.
分析 (1)直接利用a的取值范围化简求出答案;
(2)利用a,b的取值范围,进而化简二次根式即可.
解答 解:(1)由题意可得:①当a>0时$\sqrt{{a}^{2}}$=a;②当a<0时$\sqrt{{a}^{2}}$=-a;
故答案为:a,-a;
(2)如图所示:-2<a<-1,0<b<1,
则$\sqrt{a^2}$-$\sqrt{b^2}$-$\sqrt{{{(a+b)}^2}}$=-a-b+(a+b)=0.
点评 此题主要考查了二次根式的性质与化简以及实数与数轴,正确化简二次根式是解题关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
12.抛物线y=x2-2的顶点坐标为( )
| A. | (0,-2) | B. | (-2,0) | C. | (0,2) | D. | (2,0) |
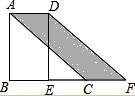 如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.
如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.
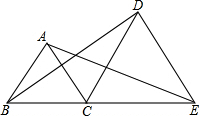 点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.
点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB. 如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).
如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).