��Ŀ����
10����ͼ�٣�ƽ��ֱ������ϵ�У�����OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ���B������Ϊ��2��4����������OABC���ŵ�A˳ʱ����ת90��õ�����AFED��ֱ��y=kx+b������G��4��0������y���ڵ�H����1����D��E������ֱ�ΪD��2��2����E��6��2����
��2����ֱ��GH����EF�е�Kʱ����ͼ�ڣ�����P�ӵ�C��������������C-B-D��ÿ��1����λ�ٶ����յ�D�˶�������PH��PG�����P�˶���ʱ��Ϊt���룩����PGH�����ΪS��ƽ����λ����
����ֱ��GH����Ӧ�ĺ�����ϵʽ��
����S��t֮��ĺ�����ϵʽ��
��3����ֱ��GH������Eʱ����ͼ�ۣ���Q������B-D-E-F�ϵĵ㣬����Q��QM��GH�ڵ�M����QN��x���ڵ�N������QMNΪ����������ʱ��ֱ��д����Q�����꣮
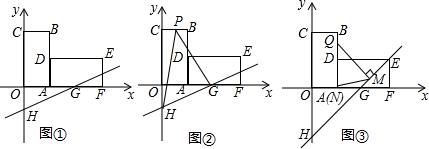
���� ��1���ɾ��ε����ʺ�ѡת�����ʼ��ɣ�
��2�����ô���ϵ�������GH�Ľ���ʽ�������ε�������������������ε�����ĺͻ����㣻
��3������һ�������˶��ص��ͼ�ε����ʣ�ȷ������Q��N��M�����꣬���������ľ��빫ʽ�����Ӧ��ȣ���QMNΪ���������Σ��������������������⣬���ɣ�
�����������жϳ���EGF=��FEG=��DEG=45�㣬�ٷ��������ۼ��㼴�ɵó����ۣ�
��� �⣺��1���߾���OABC���ŵ�A˳ʱ����ת90��õ�����AFED����B��2��4����
��OA=AD=2��OC=AF=4��
��D��2��2����E��6��2����
�ʴ�ΪD��2��2����E��6��2����
��2���ٽ⣺��E��6��2����G��4��0����
��K��6��1����
��ֱ��y=kx+b������G��K��
��$\left\{\begin{array}{l}{6k+b=1}\\{4k+b=0}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$��
��ֱ��GH�Ľ���ʽΪy=$\frac{1}{2}$x-2��
�ڵ�0��t��2ʱ���ӳ�CB��HG��W����ͼ�٣�
S��PHG=S��SHW-S��HCP-S��PGW=$\frac{1}{2}$[[6��12-6t-4��12-t��]=-t+12��
�ڵ�2��t��4ʱ���ӳ�BA��HG��T����ͼ�ڣ�
S��PHG=S��PTH+S��PGT=$\frac{1}{2}$��4��7-t��=-2t+14��
��3������һ���ٵ�0��t��2ʱ����ͼ�ۣ�
�����⣬��N��2��0����Q��2��4-t����
��G��4��0����E��6��2����
��ֱ��HE�Ľ���ʽΪy=x-4�٣�
��QM��HE��
��ֱ��QM�Ľ���ʽy=-x+6-t�ڣ�
�����٢ڵã�M��$\frac{10-t}{2}$��$\frac{2-t}{2}$����
��QN2=��4-t��2��MN2=$\frac{{��t-6��}^{2}}{4}$+$\frac{��2-t��^{2}}{4}$��QM2=$\frac{��t-6��^{2}}{2}$��
������QN=QMʱ����QN2=QM2��
�ࣨ4-t��2=$\frac{{��t-6��}^{2}}{4}$+$\frac{��2-t��^{2}}{4}$��
��t=2��t=6���ᣩ��
��Q��2��2��
������QN=QMʱ������ͬ����һ������t=2��2$\sqrt{2}$���ᣩ��
������MN=QMʱ������ͬ����һ������t=4���ᣩ��
�ڵ�2��t��6ʱ��
�����⣬��N��t��0����Q��t��2����M��$\frac{t+6}{2}$��$\frac{t-2}{2}$����
�����͢٣���һ���������������
������QN=QMʱ��t=6+2$\sqrt{2}$���ᣩ����t=6-2$\sqrt{2}$��
��Q��6-2$\sqrt{2}$��2����
������QN=MNʱ��t=-8���ᣩ��t=2���ᣩ����
������QM=MNʱ��t=4��
��Q��4��2����
�۵�6��t��8ʱ��
�����⣬��N��6��0����Q��6��8-t����M��$\frac{18-t}{2}$��-$\frac{t-10}{2}$����
�����͢٣���һ���������������
������QN=QMʱ��t=10+2$\sqrt{2}$���ᣩ����t=10-2$\sqrt{2}$��
��Q��6��2$\sqrt{2}$-2����
������QN=MNʱ��t=6���ᣩ��t=10���ᣩ
������QM=MNʱ��t=8���ᣩ��
��Q��6-2$\sqrt{2}$��2����Q��2��2����Q��4��2����Q��6��2$\sqrt{2}$-2����
����������G��4��0����E��6��2����
��ֱ��EG�Ľ���ʽΪy=x-4��
���EGF=45�㣬
���DEG=��GEF=45�㣬
����ͼ4��
����Q��BD��ʱ��
��QM��EG��
���EMQ=90�㣬
�ߡ�DEG=45�㣬
���DHQ=��EHM=45�㣬
���DQH=45�㣬
�ߡ�QMNΪ���������Σ�
�ߡ�QMN��90�㣬
��ֻ��QN=QM��
�ߡ�QAF=��QMG=90�㣬
��GN=GM=2��
��M��4+$\sqrt{2}$��$\sqrt{2}$����
��Q��2��m����
��QN=m��QM=$\sqrt{��4+\sqrt{2}-2��^{2}+��\sqrt{2}-m��^{2}}$��
��m=$\sqrt{��4+\sqrt{2}-2��^{2}+��\sqrt{2}-m��^{2}}$��
��m=4$\sqrt{2}$+4��4���ᣩ
����ͼ5��
����Q��DE�ϣ�QN=2��
��QM=QN=2ʱ����Rt��EMQ�У���QEG=45�㣬��
EQ=$\sqrt{2}$QM=2$\sqrt{2}$��
��Q��6-2$\sqrt{2}$��2����
��QM=MNʱ����M��QN�Ĵ�ֱƽ���ߣ�
���M��EG���е㣬
��Rt��EFG��FG=$\sqrt{2}$EF=2$\sqrt{2}$��
��EM=$\sqrt{2}$��
��QE=$\sqrt{2}$EM=2��
��Q��4��2����
��MN=QNʱ���ߡ�EQM=45�㣬
���MQN=45�㣬
���QNM=90�㣬
���M�͵�G�غϣ�
��AG=2��
��Q��2��2����
����ͼ6��
��Q��EF��ʱ���ߡ�EMQ=90�㣬��NEG=45�㣬
���EQM=45�㣬
���NQM=135�㣬
��ֻ��QM=QN��
��QN=x����EQ=2-x��
��Rt��EMQ��MQ=QN=x��
���ݹ��ɶ����ã�2-x=$\sqrt{2}$x��
��x=2$\sqrt{2}$-2��
��Q��6��2$\sqrt{2}$-2����
����Q��6-2$\sqrt{2}$��2����Q��2��2����Q��4��2����Q��6��2$\sqrt{2}$-2����
���� �������ı��ε��ۺ��⣬�漰�������ľ��빫ʽ������ϵ������ļ��㷽�����ֶη�������ۣ��Ȿ��Ĺؼ�����t��ʾ���������ͷ����������ļ������Ƚϴ�

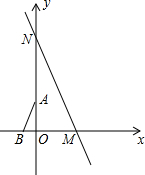 ��ͼ����ֱ������ϵ�У�ֱ��y=-$\sqrt{3}x+5\sqrt{3}$�ֱ���x�ᡢy�ύ�ڵ�M��N����A��B�ֱ���y�ᡢx���ϣ��ҡ�B=60�㣬AB=2������ABO��ԭ��O˳ʱ��ת��һ�ܣ���AB��ֱ��MNƽ��ʱ��A������Ϊ��-$\frac{3}{2}$��$\frac{\sqrt{3}}{2}$����$\frac{3}{2}$��-$\frac{\sqrt{3}}{2}$����
��ͼ����ֱ������ϵ�У�ֱ��y=-$\sqrt{3}x+5\sqrt{3}$�ֱ���x�ᡢy�ύ�ڵ�M��N����A��B�ֱ���y�ᡢx���ϣ��ҡ�B=60�㣬AB=2������ABO��ԭ��O˳ʱ��ת��һ�ܣ���AB��ֱ��MNƽ��ʱ��A������Ϊ��-$\frac{3}{2}$��$\frac{\sqrt{3}}{2}$����$\frac{3}{2}$��-$\frac{\sqrt{3}}{2}$����
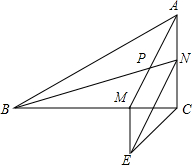 ��ͼ���ڡ�ABC�У���C=90�㣬AM��BN���ڵ�P����BM=AC��AN=CM����EMC�ǵ���ֱ�������Σ�
��ͼ���ڡ�ABC�У���C=90�㣬AM��BN���ڵ�P����BM=AC��AN=CM����EMC�ǵ���ֱ�������Σ�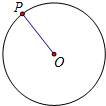 ��ͼ��ʾ����O�����Ϊ1����PΪ��O��һ�㣬��Ǻ�[n��m]��ʾ�뾶OP����ͼ��ʾ��λ�ÿ�ʼ�Ե�OΪ����������תn�κ뾶OPɨ�����������ת�Ĺ���Ϊ����1����תm�ȣ���2�δӵ�1��ֹͣ��λ������ͬ�ķ����ٴ���ת$\frac{m}{2}$�ȣ���3�δӵ�2��ֹͣ��λ������ͬ�ķ����ٴ���ת$\frac{m}{4}$�ȣ���4�δӵ�3��ֹͣ��λ������ͬ�ķ����ٴ���ת$\frac{m}{8}$�ȣ����������ƣ�����[2��90]=$\frac{3}{8}$����[2016��180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$��
��ͼ��ʾ����O�����Ϊ1����PΪ��O��һ�㣬��Ǻ�[n��m]��ʾ�뾶OP����ͼ��ʾ��λ�ÿ�ʼ�Ե�OΪ����������תn�κ뾶OPɨ�����������ת�Ĺ���Ϊ����1����תm�ȣ���2�δӵ�1��ֹͣ��λ������ͬ�ķ����ٴ���ת$\frac{m}{2}$�ȣ���3�δӵ�2��ֹͣ��λ������ͬ�ķ����ٴ���ת$\frac{m}{4}$�ȣ���4�δӵ�3��ֹͣ��λ������ͬ�ķ����ٴ���ת$\frac{m}{8}$�ȣ����������ƣ�����[2��90]=$\frac{3}{8}$����[2016��180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$��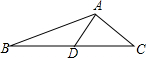 ��ͼ��ABC�У���DΪBC���е㣬AB=5��AC=3��AD=2����CD��Ϊ$\sqrt{13}$��
��ͼ��ABC�У���DΪBC���е㣬AB=5��AC=3��AD=2����CD��Ϊ$\sqrt{13}$��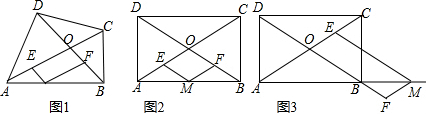
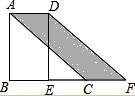 ��ͼ����֪�ڡ�ABC�У���B=90�㣬�����Ϊ12������ABC��BC�����ƶ�����DEF��λ�ã�����EΪBC���е㣬����Ӱ���֣�ƽ�б���CFD���������
��ͼ����֪�ڡ�ABC�У���B=90�㣬�����Ϊ12������ABC��BC�����ƶ�����DEF��λ�ã�����EΪBC���е㣬����Ӱ���֣�ƽ�б���CFD���������