题目内容
2.已知二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),交x轴于A,B两点,交y轴于C.则:①b=-2; ②该二次函数图象与y轴交于负半轴; ③存在这样一个a,使得M、A、C三点在同一条直线上; ④若a=1,则OA•OB=OC2.以上说法正确的有( )| A. | ①②③④ | B. | ②③④ | C. | ①②④ | D. | ①②③ |
分析 ①根据二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),代入可得a、b、c的关系,然后通过变形可以得到b的值,即可判断①是否正确;
②根据二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),代入可得a、b、c的关系,通过变形可以得到a、c的关系,由a>0,即可判断c的正负,从而可以判断②是否正确;
③求出过点M、C的直线解析式,然后令y=0,求出相应的x的值,然后将x的值代入二次函数的解析式,看是否有a的值使得二次函数的值等于,注意a的值必须大于0,从而可以判断③是否正确;
④根据a的值可以得到二次函数的解析式,从而可以推出结论是否正确.
解答 解:∵二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),
∴$\left\{\begin{array}{l}{a-b+c=2}&{①}\\{a+b+c=-2}&{②}\end{array}\right.$
②-①,得2b=-4,
解得b=-2,故①b=-2正确;
②+①,得2(a+c)=0,
∴a+c=0,
∵a>0,
∴c=-a<0,故②正确;
设过点M(-1,2),点C(0,c)的直线的解析式为y=kx+m
∴$\left\{\begin{array}{l}{-k+m=2}\\{m=c}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=c-2}\\{m=c}\end{array}\right.$
∴y=(c-2)x+c,
∵c=-a,
∴y=(-a-2)x-a,
当y=0时,x=$\frac{-a}{a+2}$,
将x=$\frac{-a}{a+2}$代入y=ax2-2x-a,得y=$\frac{-2{a}^{2}}{(a+2)^{2}}$,
令$\frac{-2{a}^{2}}{(a+2)^{2}}$=0,得a=0,
∵a>0,∴a=0不符题意,故③错误;
当a=1时,二次函数的解析式为:y=x2-2x-1,
∴当y=0时,设x2-2x-1=0的两根为x1,x2,
∴${x}_{1}•{x}_{2}=\frac{-1}{1}=-1$,
∴OA•OB=|x1|•|x2|=|-1|=1=(-1)2=OC2,故④正确;
故选C.
点评 本题考查抛物线与x轴的交点,解题的关键是明确题意,利用数形结合的思想,找出所求结论需要的条件,可以判断所求结论是否正确.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | 当a<1时,点B在⊙A外 | B. | 当1<a<5时,点B在⊙A内 | ||
| C. | 当a<5时,点B在⊙A内 | D. | 当a>5时,点B在⊙A外 |
| A. | (0,-2) | B. | (-2,0) | C. | (0,2) | D. | (2,0) |
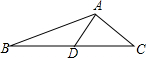 如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.
如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.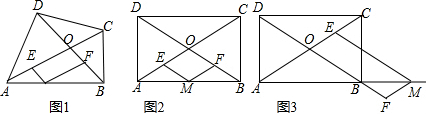
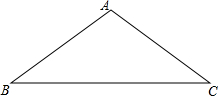 如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.
如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.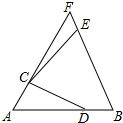 如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.
如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.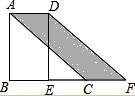 如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.
如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.