题目内容
8.阅读下面解题过程:已知关于x的不等式(2a-b)x+a-5b>0的解集为x<$\frac{10}{7}$,求关于x的不等式ax>b的解集.
解:由题意得2a-b<0,解不等式得x<$\frac{5b-a}{2a-b}$.
由题意得$\frac{5b-a}{2a-b}$=$\frac{10}{7}$,解得b=$\frac{3}{5}$a.
因为2a-b<0,所以2a-$\frac{3}{5}$a<0,
即a<0,所以ax>b的解集为x<$\frac{b}{a}$,即x<$\frac{3}{5}$.
根据下面的解题思路解出下题.
关于x的不等式(2a-b)x>a-2b的解集为x<$\frac{5}{2}$,求关于x的不等式ax+b<0的解集.
分析 仿照例题求解:先利用不等式(2a-b)x>a-2b的解集为x<$\frac{5}{2}$可判断2a-b<0,则解不等式得x<$\frac{a-2b}{2a-b}$,所以$\frac{a-2b}{2a-b}$=$\frac{5}{2}$,解得b=8a,接着判断a<0,然后解ax+b<0.
解答 解:由题意得2a-b<0,解不等式得x<$\frac{a-2b}{2a-b}$
由题意得$\frac{a-2b}{2a-b}$=$\frac{5}{2}$,解得b=8a.
因为2a-b<0,
所以2a-8a<0,即a<0,
所以ax+b<0的解集为x>-$\frac{b}{a}$,即x>-8.
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目

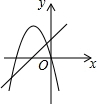
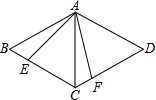 如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F.
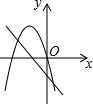
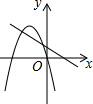
如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F. 已知抛物线y1=-(x+1)2+4.
已知抛物线y1=-(x+1)2+4.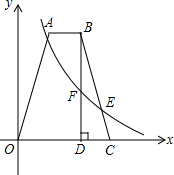 如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.
如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.