题目内容
3. 已知抛物线y1=-(x+1)2+4.
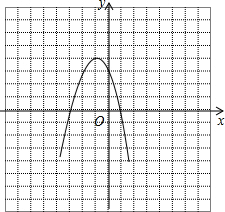
已知抛物线y1=-(x+1)2+4.(1)在坐标系上画出抛物线y1的图象;
(2)另一条抛物线y2与抛物线y1=-(x+1)2+4关于y轴对称,则抛物线y2的解析式:y2=(x+1)2-4;
(3)两条抛物线顶点间的距离是8.
分析 (1)利用列表、描点、连线即可画出这条抛物线.
(2)由关于x轴对称点的特点是:横坐标不变,纵坐标变为相反数,可求出抛物线y=-(x+1)2+4关于x轴对称的抛物线解析式.
(3)求得抛物线y1=-(x+1)2+4的顶点坐标,然后根据轴对称的性质即可求得两顶点间的距离.
解答 解:(1)列表:
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | … |
 ;
;(2)∵y1=-(x+1)2+4,
∴关于x轴对称的抛物线解析式为-y=-(x+1)2+4,即y2=(x+1)2-4;
故答案为y2=(x+1)2-4.
(3)∵抛物线y1=-(x+1)2+4的顶点为(-1,4),
∴两顶点间的距离为8.
故答案为8.
点评 此题考查了二次函数的图象与几何变换,正确理解轴对称的性质是解决问题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
14.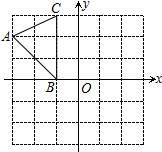 如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将
如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将
△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A、B、C的
对应点分别A1、B1、C1,则点A1的坐标为( )
 如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将
如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A、B、C的
对应点分别A1、B1、C1,则点A1的坐标为( )
| A. | (3,-3) | B. | (1,-1) | C. | (3,0) | D. | (2,-1) |
 如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$.
如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$.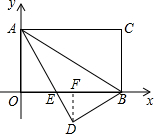 如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.
如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.