题目内容
5.已知一个二次函数f(x),f(1)=3,f(0)=1,f(-1)=1,求这个二次函数.分析 设抛物线的解析式为y=ax2+bx+c,把三点分别代入根据待定系数法就求得.
解答 解:设抛物线的解析式为y=ax2+bx+c,
将(1,3),(0,1),(-1,1)代入得,
$\left\{\begin{array}{l}{a+b+c=3}\\{c=1}\\{a-b+c=1}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=1}\\{b=1}\\{c=1}\end{array}\right.$,
∴y=x2+x+1,
即f(x)=x2+x+1.
点评 本题考查了待定系数法求二次函数的解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
17.下列计算中正确的是( )
| A. | (x-1)-2=x2 | B. | x2n÷x2=xn(n是正整数) | ||
| C. | (-2x2)3=-6x6 | D. | (-3a-2)(3a-2)=9a2-4 |
15.去年体育测试中,从某校初三(1)班中抽取男、女生各15名进行三项体育成绩复查测试,在这个问题中,下列叙述正确的是( )
| A. | 该校所有初三学生是总体 | |
| B. | 所抽取的30名学生是样本 | |
| C. | 所抽取的15名学生是样本 | |
| D. | 所抽取的30名学生的体育成绩是样本 |
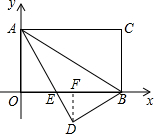 如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.
如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.