Question

16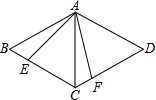．如图，AC是菱形ABCD的对角线，∠B=60°，以点A为顶点作∠EAF=60°，∠EAF的两边分别交BC，CD于点E，F．
求证：△ABE≌△ACF．

Answer 1

分析 利用菱形的性质得出AB=BC，则△ABC是等边三角形，进而得出∠BAE=∠CAF，即可得出△ABE≌△ACF．

解答 证明：∵AC是菱形ABCD的对角线，∠B=60°，
∴AB=BC，则△ABC是等边三角形，
∴∠BAC=∠ACD=∠ACB=60°，AB=AC，
∵∠EAF=60°，
∴∠BAE+∠EAC=∠AEC+∠CAF，
∴∠BAE=∠CAF，
在△ABE和△ACF中
∵$\left\{\begin{array}{l}{∠B=∠ACF}\\{AB=AC}\\{∠BAE=∠CAF}\end{array}\right.$，
∴△ABE≌△ACF（ASA）．

点评 此题主要考查了菱形的性质以及全等三角形的判定与性质，得出∠BAE=∠CAF是解题关键．