题目内容
19.二次函数y=ax2+bx与一次函数y=ax+b(a≠0)在同一平面直角坐标系中可能的图象为( )| A. |  | B. | 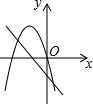 | C. | 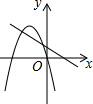 | D. | 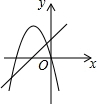 |
分析 根据二次函数y=ax2+bx与一次函数y=ax+b(a≠0)可以求得它们的交点坐标,从而可以判断哪个选项是正确的.
解答 解:$\left\{\begin{array}{l}{y=a{x}^{2}+bx}\\{y=ax+b}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=-\frac{b}{a}}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=a+b}\end{array}\right.$.
故二次函数y=ax2+bx与一次函数y=ax+b(a≠0)在同一平面直角坐标系中的交点在x轴上或点(1,a+b).
故选A.
点评 本题考查二次函数的图象、一次函数的图象,解题的关键是明确二次函数与一次函数图象的特点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球.下列事件是必然事件的是( )
| A. | 摸出的三个球中至少有两个球是黑球 | |
| B. | 摸出的三个球中至少有两个球是白球 | |
| C. | 摸出的三个球中至少有一个球是黑球 | |
| D. | 摸出的三个球中至少有一个球是白球 |
7.已知∠α和∠β互为余角.若∠α=40°,则∠β等于( )
| A. | 40° | B. | 50° | C. | 60° | D. | 140° |
14.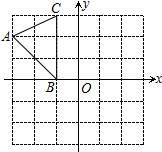 如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将
如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将
△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A、B、C的
对应点分别A1、B1、C1,则点A1的坐标为( )
 如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将
如图,在平面直角坐标系中,A(-3,2)、B(-1,0)、C(-1,3),将△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A、B、C的
对应点分别A1、B1、C1,则点A1的坐标为( )
| A. | (3,-3) | B. | (1,-1) | C. | (3,0) | D. | (2,-1) |
 已知:如图,四边形BCDE是矩形,AB=AC,求证:AE=AD.
已知:如图,四边形BCDE是矩形,AB=AC,求证:AE=AD. 如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$.
如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$.