题目内容
16.某体育用品商店销售一种品牌的羽毛球拍和配套的羽毛球,购买一副羽毛球拍和一筒羽毛球共需60元,购买两幅羽毛球拍和3筒羽毛球共需130元.(1)求每副羽毛球拍和每筒羽毛球的价钱;
(2)春季运动会召开前夕,该商店开展了两种优惠促销活动,具体办法如下:
活动甲:买一副羽毛球拍送一筒羽毛球;
活动乙:按购买金额打9折付款.
学校欲购买这种羽毛球拍10副,羽毛球x(x≥10)筒.
①写出每种优惠办法实际付款金额y甲(元),y乙(元)与x(筒)之间的函数关系式.
②比较购买同样多的羽毛球时,按哪种优惠付款更省钱?
③如果商场允许可以任意选择一种优惠办法购买,也可以同时用两种优惠方法购买,请你就购买这种羽毛球拍10副和羽毛球60筒设计一种最省钱的购买方案.
分析 (1)根据购买一副羽毛球拍和一筒羽毛球共需60元,购买两幅羽毛球拍和3筒羽毛球共需130元列出方程组解答即可;
(2)①根据题意列出函数关系式即可;
②根据两种函数解析式组成不等式解答即可;
③把购买这种羽毛球拍10副和羽毛球60筒代入两种解析式中进行比较即可.
解答 解:(1)每副羽毛球拍和每筒羽毛球的价钱为x和y元,可得:
$\left\{\begin{array}{l}{x+y=60}\\{2x+3y=130}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=10}\end{array}\right.$,
答:每副羽毛球拍和每筒羽毛球的价钱为50元和10元;
(2)①设羽毛球x筒,可得:
y甲(元)与x(筒)之间的函数关系式为:y甲=10×50+(x-10)×10=10x+400,
y乙(元)与x(筒)之间的函数关系式为:y乙=10×0.9×50+0.9×10x=9x+450;
②根据题意可得:10x+400=9x+450,
解得:x=50,
所以当x>50时,活动乙优惠;
当x=50时,两种相同;
当x<50时,活动甲优惠;
③甲方案:50×10+50×10=1000元;
乙方案:(50×10+60×10)×0.9=990元;
两种方案买:50×10+50×10×0.9=950元,
所以用甲方案买羽毛球拍10副,剩下用乙方案购买.
点评 本题考查了一次函数的实际应用,解决本题的关键是读懂题意,找到符合题意的不等关系式,及所求量的等量关系.要会用分类的思想来讨论求得方案的问题.

练习册系列答案
相关题目
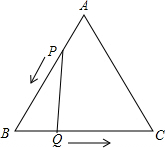 如图所示,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题:
如图所示,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题: 如图,在△ABC中,∠C为钝角,分别以AB,AC,BC为边作正方形,若AB=$\frac{9}{2}$,AC=2,BC=3,S3-S1=6,则S4-S2的值是$\frac{5}{4}$.
如图,在△ABC中,∠C为钝角,分别以AB,AC,BC为边作正方形,若AB=$\frac{9}{2}$,AC=2,BC=3,S3-S1=6,则S4-S2的值是$\frac{5}{4}$. 将正奇数按如右上图所示规律排列下去.若用有序数对(n,m)表示实数9,则(6,3)表示的数是35.2011是(45,16).
将正奇数按如右上图所示规律排列下去.若用有序数对(n,m)表示实数9,则(6,3)表示的数是35.2011是(45,16).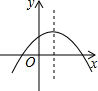 已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,则正比例函数y=(b+c)x的图象与反比例函数y=$\frac{a}{x}$的图象在同一坐标系中可能是( )
已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,则正比例函数y=(b+c)x的图象与反比例函数y=$\frac{a}{x}$的图象在同一坐标系中可能是( )


