题目内容
4.观察下列各式:$\frac{{3}^{2}}{{2}^{2}-1}=\frac{3}{2-1}$,$\frac{{4}^{2}}{{3}^{2}-1}=\frac{4}{3-1}$,…,设n表示正整数(n≥3),用含n的代数式表示这个规律为$\frac{(n+1)^{2}}{{n}^{2}-1}$=$\frac{n+1}{n-1}$.分析 把分母用平方差公式因式分解,进一步和分子约分即可得出结论.
解答 解:∵$\frac{{3}^{2}}{{2}^{2}-1}=\frac{3}{2-1}$,$\frac{{4}^{2}}{{3}^{2}-1}=\frac{4}{3-1}$,…,
∴$\frac{(n+1)^{2}}{{n}^{2}-1}$=$\frac{n+1}{n-1}$.
故答案为:$\frac{(n+1)^{2}}{{n}^{2}-1}$=$\frac{n+1}{n-1}$.
点评 此题考查数字的变化规律,利用平方差公式因式分解找出运算的规律是解决问题的关键.

练习册系列答案
相关题目
10.关于x的一元二次方程a(b-c)x2+b(c-a)x+c(a-b)=0必有一个根为( )
| A. | x=0 | B. | x=1 | C. | x=-1 | D. | x=2 |
7.计算(-56)×0÷(-28)-(-5)的结果是( )
| A. | -5 | B. | 5 | C. | 7 | D. | -3 |
13.2015年6月15日为全国低碳日,2015年全国低碳日活动主题为“低碳城市-宜居可持续”,某市相关部门为了进行全国低碳日的宣传活动,需要制作一批宣传单,现有甲、乙两家印刷社可供选择,甲、乙两家印刷社印制此种宣传单的收费标准如下(总费用=制版费+印刷费).
乙印刷社的制版费为60元,印刷费的收费方式为:500张以内(包括500张),按每张0.9元收费,超过500张的部分,按每张0.85元收费.
(1)求在甲印刷社印制宣传单时,总费用w(元)与印制数x(张)之间的函数关系式;
(2)若该部门在乙印刷社印制了1000张宣传单,求所花的总费用;
(3)该部门印制多少张宣传单时,在乙印刷社印制比较合算?
| 印制数x(张) | … | 50 | 100 | 150 | … |
| 印刷费y(元) | … | 45 | 90 | 135 | … |
(1)求在甲印刷社印制宣传单时,总费用w(元)与印制数x(张)之间的函数关系式;
(2)若该部门在乙印刷社印制了1000张宣传单,求所花的总费用;
(3)该部门印制多少张宣传单时,在乙印刷社印制比较合算?
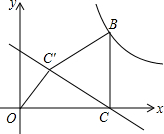 点C在x的正半轴上,且BC⊥OC于点C,将线段BC绕点B顺时针旋转60°至BC′位置,且点C′的坐标为(2,2$\sqrt{3}$).
点C在x的正半轴上,且BC⊥OC于点C,将线段BC绕点B顺时针旋转60°至BC′位置,且点C′的坐标为(2,2$\sqrt{3}$).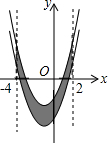 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向下平移,平移后的抛物线和原抛物线与经过点(-4,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则s与m的函数关系式为s=6m(不写自变量取值范围).
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向下平移,平移后的抛物线和原抛物线与经过点(-4,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则s与m的函数关系式为s=6m(不写自变量取值范围).