题目内容
8.某汽车制造公司计划生产A、B两种新型汽车共40辆投放到市场销售.已知A型汽车每辆成本34万元,售价39万元;B型汽车每辆成本42万元,售价50万元.若该公司对此项计划的投资不低于1536万元,不高于1552万元.请解答下列问题:(1)该公司有哪几种生产方案?
(2)该公司按照哪种方案生产汽车,才能在这批汽车全部售出后,所获利润最大,最大利润是多少?
(3)在(2)的情况下,公司将其中5辆汽车捐赠给了某公益组织,余下的汽车全部售出,这样该公司仍获利44万元,请直接写出该公司把A、B两种型号的汽车各捐赠出几辆?
分析 (1)设A型号的轿车为x辆,可根据题意列出不等式组,根据问题的实际意义推出整数值;
(2)根据“利润=售价-成本”列出一次函数的解析式解答;
(3)根据(2)中方案设计计算.
解答 解:(1)设A型号的轿车为x辆,由题意得1536≤34x+42(40-x)≤1552,
解得16≤x≤18,
∵x是正整数,
∴x=16或17或18.
有以下生产三种方案:
①生产A型号的轿车16辆,B型24辆;
②生产A型号的轿车17辆,B型23辆;
③生产A型号的轿车18辆,B型22辆.
(2)设所获利润为y元,由题意有:
y=(39-34)x+(50-42)(40-x)=-3x+320,
∵y随x的增大而减小,
∴x=16时,
∴y最大值=272,
∴最大利润272万元.
(3)因为利润与A型号的轿车之间的关系为:y=-3x+320.
当生产A型号的轿车16辆、B型24辆时,设A型号的汽车捐赠x辆,可得:
(16-x)×5+[24-(5-x)]×8-34x-42(5-x)=44,
解得:x=2.
答:A型号的汽车捐赠出2辆,B型号的汽车捐赠出3辆.
点评 此题主要考查了一次函数的应用,以及一元一次不等式组的应用,此题是典型的数学建模问题,要先将实际问题转化为不等式组解应用题.

练习册系列答案
相关题目
13.2015年6月15日为全国低碳日,2015年全国低碳日活动主题为“低碳城市-宜居可持续”,某市相关部门为了进行全国低碳日的宣传活动,需要制作一批宣传单,现有甲、乙两家印刷社可供选择,甲、乙两家印刷社印制此种宣传单的收费标准如下(总费用=制版费+印刷费).
乙印刷社的制版费为60元,印刷费的收费方式为:500张以内(包括500张),按每张0.9元收费,超过500张的部分,按每张0.85元收费.
(1)求在甲印刷社印制宣传单时,总费用w(元)与印制数x(张)之间的函数关系式;
(2)若该部门在乙印刷社印制了1000张宣传单,求所花的总费用;
(3)该部门印制多少张宣传单时,在乙印刷社印制比较合算?
| 印制数x(张) | … | 50 | 100 | 150 | … |
| 印刷费y(元) | … | 45 | 90 | 135 | … |
(1)求在甲印刷社印制宣传单时,总费用w(元)与印制数x(张)之间的函数关系式;
(2)若该部门在乙印刷社印制了1000张宣传单,求所花的总费用;
(3)该部门印制多少张宣传单时,在乙印刷社印制比较合算?
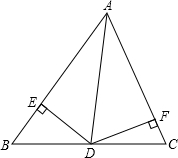 如图,在△ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积为45cm2,则DE的长为5cm.
如图,在△ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积为45cm2,则DE的长为5cm.