题目内容
5. 如图,⊙O的直径AB垂直于弦CD于点E,∠A=22.5°,OC=2,则CD的长为2$\sqrt{2}$.
如图,⊙O的直径AB垂直于弦CD于点E,∠A=22.5°,OC=2,则CD的长为2$\sqrt{2}$.
分析 由同圆的半径相等得∠A=∠OCA=22.5°,根据外角定理求∠BOC=45°,得到△CEO是等腰直角三角形,由
OC=2求CE的长,最后由垂径定理得出结论.
解答 解:∵OC=OA,∠A=22.5°,
∴∠A=∠OCA=22.5°,
∵∠BOC=∠A+∠OCA=45°,
∵CD⊥AB,
∴∠CEO=90°,
∴△CEO是等腰直角三角形,
∵CO=2,
∴CE=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∵CD⊥AB,
∴CD=2CE=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题是圆的计算题,考查了垂径定理和勾股定理的运用,是常考题型;熟练掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧;在圆中的计算问题中,因为常有直角三角形存在,常利用勾股定理求线段的长.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19. 如图,AB=AC,D、E在AB,AC上,∠B=∠C,下列结论:
如图,AB=AC,D、E在AB,AC上,∠B=∠C,下列结论:
(1)BE=CD
(2)△BOD≌△COE
(3)CD⊥AB,BE⊥AC
(4)OA平分∠BAC,
其中,结论一定成立的有( )
 如图,AB=AC,D、E在AB,AC上,∠B=∠C,下列结论:
如图,AB=AC,D、E在AB,AC上,∠B=∠C,下列结论:(1)BE=CD
(2)△BOD≌△COE
(3)CD⊥AB,BE⊥AC
(4)OA平分∠BAC,
其中,结论一定成立的有( )
| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (1)(3)(4) | D. | (1)(2)(4) |
17.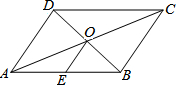 如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
 如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |

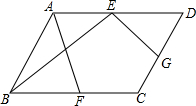 在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,则AF的长为4.
在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,则AF的长为4.