题目内容
10.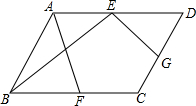 在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,则AF的长为4.
在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,则AF的长为4.
分析 连接AC、EC,由平行四边形的性质得出AD=BC,AD∥BC,证明四边形AFCE是平行四边形,得出AF=CE,由平行线得出$\frac{AQ}{CQ}$=$\frac{EQ}{BQ}$=$\frac{AE}{BC}$=$\frac{1}{2}$,
,设AQ=a,EQ=b,则CQ=2a,BQ=2b,证明EG是△ACD的中位线,由三角形中位线定理得出EG∥AC,得出BE⊥AC,由勾股定理得得出方程,求出a2=$\frac{11}{3}$,得出BQ2=4b2=$\frac{16}{3}$,b2=$\frac{4}{3}$,在Rt△EQC中,由勾股定理求出CE,即可得出AF的长.
解答 解:连接AC、EC,如图所示:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E,F分别是AD,BC,CD的中点,
∴AE=CE,
∴四边形AFCE是平行四边形,
∴AF=CE,
∵AD∥BC,
∴$\frac{AQ}{CQ}$=$\frac{EQ}{BQ}$=$\frac{AE}{BC}$=$\frac{1}{2}$,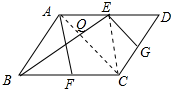
设AQ=a,EQ=b,则CQ=2a,BQ=2b,
∵点E,G分别是AD,CD的中点,
∴EG是△ACD的中位线,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
由勾股定理得:AB2-AQ2=BC2-CQ2,
即9-a2=(2$\sqrt{5}$)2-4a2,
∴3a2=11,
∴a2=$\frac{11}{3}$,
∴BQ2=4b2=(2$\sqrt{5}$)2-4×$\frac{11}{3}$=$\frac{16}{3}$,
∴b2=$\frac{16}{3}$×$\frac{1}{4}$=$\frac{4}{3}$,
在Rt△EQC中,CE2=EQ2+CQ2=b2+4a2=16,
∴CE=4,
∴AF=4.
故答案为:4.
点评 本题考查了平行四边形的性质与判定、三角形中位线定理、勾股定理;熟练掌握平行四边形的判定与性质,运用勾股定理进行计算是解决问题的关键,本题综合性强,有一定难度.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | xy+2=1 | B. | x2+$\frac{1}{2x}$-9=0 | C. | ax2+bx+c=0 | D. | 2x2=3x-3 |
 如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )
如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )| A. | (-3-2$\sqrt{3}$,0) | B. | (3,0) | C. | (-1,0) | D. | (2$\sqrt{3}$,0) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 七次多项式 | B. | 四次多项式 | ||
| C. | 三次多项式 | D. | 四次多项式或四次单项式 |
 如图,⊙O的直径AB垂直于弦CD于点E,∠A=22.5°,OC=2,则CD的长为2$\sqrt{2}$.
如图,⊙O的直径AB垂直于弦CD于点E,∠A=22.5°,OC=2,则CD的长为2$\sqrt{2}$.