题目内容
19. 如图,AB=AC,D、E在AB,AC上,∠B=∠C,下列结论:
如图,AB=AC,D、E在AB,AC上,∠B=∠C,下列结论:(1)BE=CD
(2)△BOD≌△COE
(3)CD⊥AB,BE⊥AC
(4)OA平分∠BAC,
其中,结论一定成立的有( )
| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (1)(3)(4) | D. | (1)(2)(4) |
分析 根据AB=AC,∠B=∠C,∠A=∠A,判定△ABE≌△ACD,再根据全等三角形的性质得出对应边相等,对应角相等,进而得出结论.
解答 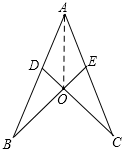 解:∵AB=AC,∠B=∠C,∠A=∠A,
解:∵AB=AC,∠B=∠C,∠A=∠A,
∴△ABE≌△ACD,
∴AD=AE,
又∵AB=AC,
∴BD=CE,故结论(1)正确;
又∵∠BOD=∠COE,∠B=∠C,
∴△BOD≌△COE,故(2)正确;
∵∠ADC与∠AEB不一定都是直角,故结论(3)CD⊥AB,BE⊥AC不一定成立;
连接AO,
∵△BOD≌△COE,
∴BO=CO,
又∵AB=AC,AO=AO,
∴△AOB≌△AOC,
∴∠BAO=∠CAO,
∴故结论(4)OA平分∠BAC正确.
故选(D)
点评 本题主要考查了全等三角形的判定与性质,解决问题的关键是得出三角形全等后,再根据全等三角形的性质可得线段相等,或角相等.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
9.已知关于x的方程x2+2a=5的一个解是-1,则a的值为( )
| A. | 1 | B. | 2 | C. | ±1 | D. | ±2 |
14.小明身高为1.6米,他在距路灯5米处的位置发现自己的影长为1米,他在向前走距离路灯为7米时,他的影长将( )
| A. | 增长0.4米 | B. | 减少0.4米 | C. | 增长1.4米 | D. | 减少1.4米 |
4.下列方程中是一元二次方程的是( )
| A. | xy+2=1 | B. | x2+$\frac{1}{2x}$-9=0 | C. | ax2+bx+c=0 | D. | 2x2=3x-3 |
 如图,点E在?ABCD的边BC上,BE=CD.若∠EAC=20°,∠B+∠D=80°,则∠ACD的度数为90°.
如图,点E在?ABCD的边BC上,BE=CD.若∠EAC=20°,∠B+∠D=80°,则∠ACD的度数为90°. 二次函数y=-x2+bx+c的图象如图所示
二次函数y=-x2+bx+c的图象如图所示 如图,⊙O的直径AB垂直于弦CD于点E,∠A=22.5°,OC=2,则CD的长为2$\sqrt{2}$.
如图,⊙O的直径AB垂直于弦CD于点E,∠A=22.5°,OC=2,则CD的长为2$\sqrt{2}$.