题目内容
15.不等式组$\left\{\begin{array}{l}2x-1>4\\ x-6≤-2\end{array}\right.$的整数解是3和4.分析 解不等式组得出x的取值范围,再取其内的整数即可得出结论.
解答 解:$\left\{\begin{array}{l}{2x-1>4①}\\{x-6≤-2②}\end{array}\right.$.
解不等式①得:x>$\frac{5}{2}$;
解不等式②得:x≤4.
∴不等式组的解为$\frac{5}{2}$<x≤4,
∴不等式组$\left\{\begin{array}{l}2x-1>4\\ x-6≤-2\end{array}\right.$的整数解是3和4.
点评 本题考查了一元一次不等式组的整数解,熟练掌握一元一次不等式组的解法是解题的关键.

练习册系列答案
相关题目
3. 如图,已知△ABC中,AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
如图,已知△ABC中,AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
 如图,已知△ABC中,AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
如图,已知△ABC中,AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )| A. | $\sqrt{6}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 5 |
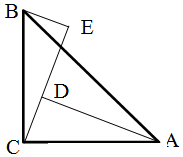 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=5cm,DE=3.4cm,则BE=1.6cm.
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=5cm,DE=3.4cm,则BE=1.6cm. 如图,AD=BC=BA,那么∠1与∠2之间的关系是2∠1+∠2=180°.
如图,AD=BC=BA,那么∠1与∠2之间的关系是2∠1+∠2=180°. 如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB、CD的距离等于4.
如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB、CD的距离等于4. 如图,点C、B、E在同一条直线上,AB∥DE,∠ACB=∠CDE,AC=CD,求证:AB=CE.
如图,点C、B、E在同一条直线上,AB∥DE,∠ACB=∠CDE,AC=CD,求证:AB=CE.