题目内容
6.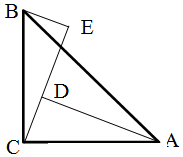 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=5cm,DE=3.4cm,则BE=1.6cm.
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=5cm,DE=3.4cm,则BE=1.6cm.
分析 可先证明△BCE≌△CAD,可求得CE=AD,结合条件可求得CD,则可求得BE.
解答 解:∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
又∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△CBE和△ACD中,$\left\{\begin{array}{l}{∠E=∠ADC}\\{∠CBE=∠ACD}\\{BC=AC}\end{array}\right.$,
∴△CBE≌△ACD(AAS),
∴BE=CD,CE=AD=5,
∵DE=3,
∴CD=CE-DE=AD-DE=5-3.4=1.6(cm),
∴BE=CD=1.6(cm).
故答案是:1.6cm.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等).

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
17.如图,四条表示方向的射线中,表示北偏西30°的是( )
| A. |  | B. |  | C. |  | D. |  |
16.若a,b,c为三角形的三边,则下列各组数据中,不能组成直角三角形的是( )
| A. | a=8,b=15,c=17 | B. | a=3,b=5,c=4 | C. | a=14,b=48,c=49 | D. | a=9,b=40,c=41 |
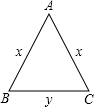 如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm)
如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm) 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y(毫克)与时间x(小时)满足:前1小时内成正比例递增,1小时后按反比例函数图象衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y(毫克)与时间x(小时)满足:前1小时内成正比例递增,1小时后按反比例函数图象衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.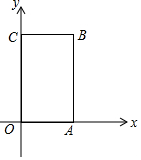 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).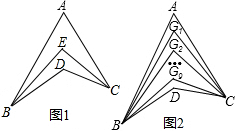
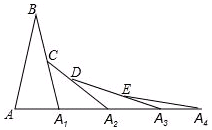 如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,…,以此类推,若∠B=20°,则∠A=$\frac{80°}{{2}^{n-1}}$.
如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,…,以此类推,若∠B=20°,则∠A=$\frac{80°}{{2}^{n-1}}$.