题目内容
10．已知有理数a，b，c满足|a-b-3|+（b+1）2+$\sqrt{c-1}$=0，求a+2b-c的值．分析 首先依据非负数的性质得到c-1=0，b+1=0，a-b-3=0，然后可求得c=1，b=-1，a=2，最后代入所求代数式进行计算即可．
解答 解：由非负数的性质可知：c-1=0，b+1=0，a-b-3=0．
解得：c=1，b=-1，a=2．
所以a+2b-c=2+2×（-1）-1=-1．
点评 本题主要考查的是非负数的性质，熟练掌握相关知识是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
20．
如图所示，横坐标是正数，纵坐标是负数的点是（ ）
如图所示，横坐标是正数，纵坐标是负数的点是（ ）| A． | A点 | B． | B点 | C． | C点 | D． | D点 |
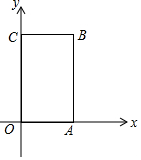如图，矩形OABC中，O为直角坐标系的原点，A、C两点的坐标分别为（3，0）、（0，5）．
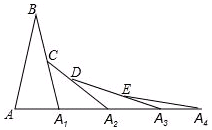如图，已知AB=A1B，A1C=A1A2，A2D=A2A3，A3E=A3A4，…，以此类推，若∠B=20°，则∠A=$\frac{80°}{{2}^{n-1}}$．
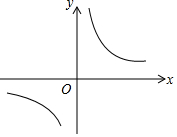已知：Rt△ABC中，∠C=90°，∠B=60°，且BC=1，若把△ABC放入如图的直角坐标系中，使斜边AB在x轴，点C在双曲线y=$\frac{\sqrt{3}}{x}$上．
2．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：
下列结论：
（1）ac＜0；
（2）抛物线顶点坐标为（1，5）；
（3）3是方程ax2+（b-1）x+c=0的一个根；
（4）当-1＜x＜3时，ax2+（b-1）x+c＞0．
其中正确的个数为（ ）
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
（1）ac＜0；
（2）抛物线顶点坐标为（1，5）；
（3）3是方程ax2+（b-1）x+c=0的一个根；
（4）当-1＜x＜3时，ax2+（b-1）x+c＞0．
其中正确的个数为（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
已知：如图△ABC中，AD⊥BC，CE⊥AB，垂足分别是D、E，AD和CE相交于O，且AD=CD．求证：BD=OD．