题目内容
5.指出下列抛物线的开口方向、对称轴和顶点坐标.(1)y=(2-x)(2x+1);
(2)y=x2+2kx+1.
分析 把抛物线解析式化为顶点式可求得开口方向、对称轴和顶点坐标.
解答 解:
(1)∵y=(2-x)(2x+1)=-2x2+3x+2=-2(x-$\frac{3}{4}$)2+$\frac{25}{8}$,
∴抛物线开口向下,对称轴为x=$\frac{3}{4}$,顶点坐标为($\frac{3}{4}$,$\frac{25}{8}$);
(2)∵y=x2+2kx+1=(x+k)2+1-k2,
∴抛物线开口向上,对称轴为x=-k,顶点坐标为(-k,1-k2).
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
相关题目
16.若a,b,c为三角形的三边,则下列各组数据中,不能组成直角三角形的是( )
| A. | a=8,b=15,c=17 | B. | a=3,b=5,c=4 | C. | a=14,b=48,c=49 | D. | a=9,b=40,c=41 |
13.已知∠A:∠B:∠C=5:2:7,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定形状 |
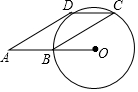 如图,A为⊙O外一点交⊙O于点B,C、D为⊙O上的两点,AD为⊙O的切线,若四边形ABCD为平行四边形,则∠A的度数为30°.
如图,A为⊙O外一点交⊙O于点B,C、D为⊙O上的两点,AD为⊙O的切线,若四边形ABCD为平行四边形,则∠A的度数为30°. 如图,在△ABC中,∠B>∠C,AE、AD分别是∠A的平分线和BC边上的高.求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
如图,在△ABC中,∠B>∠C,AE、AD分别是∠A的平分线和BC边上的高.求证:∠DAE=$\frac{1}{2}$(∠B-∠C).