题目内容
3. 如图,已知△ABC中,AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
如图,已知△ABC中,AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )| A. | $\sqrt{6}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 5 |
分析 易证△ADC≌△BDH后就可以得出BH=AC,进而可求出线段BH的长度.
解答 解:∵AD⊥BC,
∴∠ADC=∠BDH=90°,
∴∠AHE+∠DAC=90°,∠DAC+∠C=90°,
∴∠AHE=∠BHD=∠C,
在△ADC和△BDH中,
$\left\{\begin{array}{l}{∠ADC=∠BDH}\\{∠C=∠BHD}\\{AD=BD}\end{array}\right.$,
∴△ADC≌△BDH(AAS),
∴BH=AC=4,
故选B.
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时找到全等三角形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列4组线段中,不能组成直角三角形的是( )
| A. | a=3,b=4,c=5 | B. | a=2,b=3,c=4 | C. | a=5,b=12,c=13 | D. | a=8,b=15,c=17 |
13.已知∠A:∠B:∠C=5:2:7,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定形状 |
 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y(毫克)与时间x(小时)满足:前1小时内成正比例递增,1小时后按反比例函数图象衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y(毫克)与时间x(小时)满足:前1小时内成正比例递增,1小时后按反比例函数图象衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
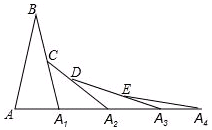 如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,…,以此类推,若∠B=20°,则∠A=$\frac{80°}{{2}^{n-1}}$.
如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,…,以此类推,若∠B=20°,则∠A=$\frac{80°}{{2}^{n-1}}$.