题目内容
13. 如图,矩形ABCD中,AB=6cm,BC=8cm,点P在AD边上移动(不与点A、D重合),过点C作BP的垂线,垂足为点Q.设BP的长为xcm,CQ的长为ycm,求y与x之间的函数关系式及自变量x的取值范围.
如图,矩形ABCD中,AB=6cm,BC=8cm,点P在AD边上移动(不与点A、D重合),过点C作BP的垂线,垂足为点Q.设BP的长为xcm,CQ的长为ycm,求y与x之间的函数关系式及自变量x的取值范围.
分析 根据两直线平行,内错角相等可得∠PBC=∠APB,再根据两组角对应相等的两个三角形相似求出△ABP和△BCQ相似,根据相似三角形对应边成比例可得$\frac{CQ}{AB}=\frac{BC}{BP}$,然后整理即可得到y与x的关系式,然后写出x的取值范围即可.
解答 解:在矩形ABCD中,AD∥BC,
∴∠PBC=∠APB,
∵∠A=∠CQB=90°,
∴△ABP∽△CQB,
∴$\frac{CQ}{AB}=\frac{BC}{BP}$,
即$\frac{y}{6}=\frac{8}{x}$,
∴y=$\frac{48}{x}$,
∵AB=6,AD=8,
∴矩形的对角线AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∴x的取值范围是6<x<10.
点评 本题利考查了相似三角形的判定及勾股定理和矩形的性质,正确的找到相似三角形并且得到对应边的比值是解题的关键.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | 要了解湖南卫视《快乐大本营》的采用普查的方法 | |
| B. | 为了解某种灯泡的使用寿命,宜采用普查的方法 | |
| C. | 为了解某班学生每天做作业的时间,宜采用普查的方法 | |
| D. | 了解外地游客对湘菜美食文化的满意度,采用普查方法 |
4. 如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )
如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )
 如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )
如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
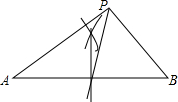 如图,有块直角三角形菜地,分配给张、王、李三家农民耕种,已知张、王、李三家人口分别为2人、4人、6人,菜地按人口比例分配,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P必须是三家地的交界地.
如图,有块直角三角形菜地,分配给张、王、李三家农民耕种,已知张、王、李三家人口分别为2人、4人、6人,菜地按人口比例分配,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P必须是三家地的交界地.