题目内容
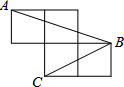如图，每个小正方形的边长为1，则∠ABC的度数为（ ）| A、90° | B、60° |
| C、45° | D、30° |
考点：勾股定理的逆定理,勾股定理,等腰直角三角形
专题：
分析：根据勾股定理即可得到AB，BC，AC的长度，进行判断即可．
解答：
解：根据勾股定理可以得到：AC=BC=
，AB=
．
∵（
）2+（
）2=（
）2．
∴AC2+BC2=AB2．
∴△ABC是等腰直角三角形．
∴∠ABC=45°．
故选：C．
解：根据勾股定理可以得到：AC=BC=| 5 |
| 10 |
∵（
| 5 |
| 5 |
| 10 |
∴AC2+BC2=AB2．
∴△ABC是等腰直角三角形．
∴∠ABC=45°．
故选：C．
点评：本题考查了勾股定理与勾股定理逆定理的运用，判断△ABC是等腰直角三角形是解决本题的关键．
练习册系列答案
相关题目
已知二次函数y=x2-2x+3+k的图象上有三点A（
，y1）、B（3，y2）、C（-
，y3），则y1、y2、y3的大小关系是（ ）
| 3 |
| 2 |
| A、y1＞y2＞y3 |
| B、y2＞y1＞y3 |
| C、y3＞y1＞y2 |
| D、y3＞y2＞y1 |
若点（a，a-3）在第四象限，则点（-a，a-4）在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图，已知某经济开发区有一块四边形空地ABCD，现计划在该空地上种植草皮，经测量∠B=90°，AB=300m，AD=400m，CD=1300m，BC=1200m．请计算种植草皮的面积．函数y=
的自变量x的取值范围在数轴上可表示为（ ）
| 2 | ||
|
A、 |
B、 |
C、 |
D、 |