题目内容
一只不透明的袋子中装有2只红球,1只白球,除颜色外都相同.
(1)从袋中任取一球,摸到红球的概率是 ;
(2)从袋中任取一球,记下颜色后放回袋中,再摸出,记下颜色后,再放回…,如此反复两次,用画树状图或列表方法求两次全部摸到白球的概率;
(3)在(2)中,求“至少有一次摸到红球”的概率= ,这个概率非常 (填“大”或“小”),说明两次摸球中 (填“一定”或“不一定”)摸到红球.
(1)从袋中任取一球,摸到红球的概率是
(2)从袋中任取一球,记下颜色后放回袋中,再摸出,记下颜色后,再放回…,如此反复两次,用画树状图或列表方法求两次全部摸到白球的概率;
(3)在(2)中,求“至少有一次摸到红球”的概率=
考点:列表法与树状图法
专题:计算题
分析:(1)直接根据概率公式求解;
(2)先画树状图展示所有种等可能的结果数,再找两次都是白球所占的结果数,然后根据概率公式求解;
(3)由于“至少有一次摸到红球”占8种可能,原式得到“至少有一次摸到红球”的概率为
,这个概率虽然非常大,但摸到红球还是随机事件,所以两次摸球中不一定摸到红球.
(2)先画树状图展示所有种等可能的结果数,再找两次都是白球所占的结果数,然后根据概率公式求解;
(3)由于“至少有一次摸到红球”占8种可能,原式得到“至少有一次摸到红球”的概率为
| 8 |
| 9 |
解答:解:(1)从袋中任取一球,摸到红球的概率=
;
(2)画树状图为:
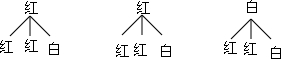
共有9种等可能的结果数,其中两次都是白球的占1种,
所以两次全部摸到白球的概率=
;
(3)“至少有一次摸到红球”的概率=
;这个概率非常大,说明两次摸球中不一定摸到红球.
故答案为
;
,大,不一定.
| 2 |
| 3 |
(2)画树状图为:

共有9种等可能的结果数,其中两次都是白球的占1种,
所以两次全部摸到白球的概率=
| 1 |
| 9 |
(3)“至少有一次摸到红球”的概率=
| 8 |
| 9 |
故答案为
| 2 |
| 3 |
| 8 |
| 9 |
点评:本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求解.

练习册系列答案
相关题目
下列实数中,无理数的是( )
A、
| ||
| B、π | ||
C、
| ||
| D、|-2| |
已知二次函数y=x2-2x+3+k的图象上有三点A(
,y1)、B(3,y2)、C(-
,y3),则y1、y2、y3的大小关系是( )
| 3 |
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y3>y1>y2 |
| D、y3>y2>y1 |